Question

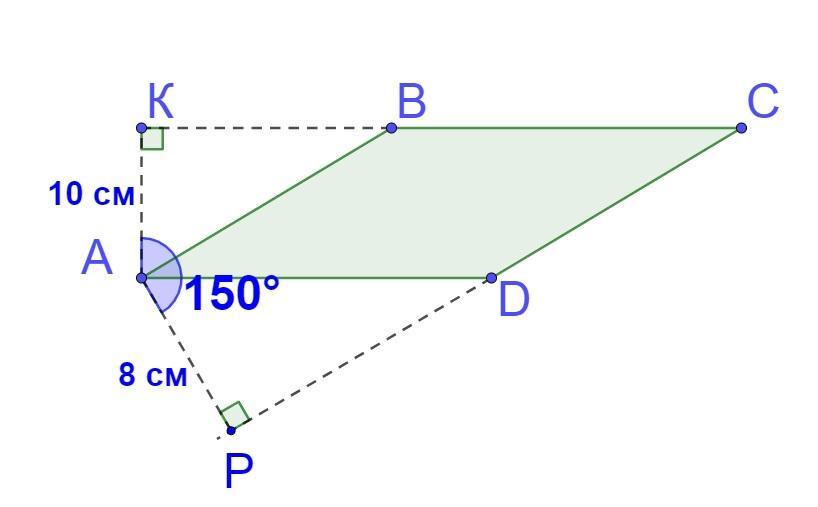
9. Висоти АК і AP паралелограма ABCD дорівнюють 10 см і 8 см відповідно. А кут КАР=150° Знайдіть площу паралелограма ABCD. Розв'язати з малюнком.​

Answer 1

Ответ:

Площа паралелограма дорівнює 160 cм²

Объяснение:

Висоти АК і AP паралелограма ABCD дорівнюють 10 см і 8 см відповідно. А кут КАР=150° Знайдіть площу паралелограма ABCD.

• Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині.

Розв'язання

1) За властивістю висот паралелограма (тупий кут перетину висот дорівнює тупому куту паралелограма), маємо, що ∠АВС=∠АDC=150° (протилежні кути паралелограма рівні).

2) Так як сума кутів паралелограма, прилеглих до кожної сторони паралелограма, дорівнює 180°, то:

∠ВАD=180°-∠АВС=180°-150°=30°

3) ∠КВА+∠АВС=180° - як суміжні, тому:

∠КВА=180°-∠АВС=180°-150°=30°

4) ∠ADP+∠АDС=180° - як суміжні, тому:

∠ADP=180°-∠АDС=180°-150°=30°

5) У ΔАКВ(∠К=90°) катет АК лежить навпроти кута ∠КВА=30°, тому він дорівнює половині гіпотенузи АВ (властивість прямокутного трикутника). Отже:

АВ=2·АК=2·10=20 (см)

6) У ΔАPD(∠D=90°) катет АP лежить навпроти кута ∠ADP=30°, тому він дорівнює половині гіпотенузи АD. Отже:

АD=2·АP=2·8=16 (см)

7) Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними:

$\bf S_{ABCD}=AB \cdot AD \cdot sin \angle BAD$

$S_{ABCD}=20 \cdot 16 \cdot sin \angle 30^\circ=320 \cdot \dfrac{1}{2} =160$  (см²)

Відповідь: 160 см²

#SPJ1