Ответы
Ответ дал:
7
Ответ:
Довели, що ∠DAC=∠BCA
Объяснение:
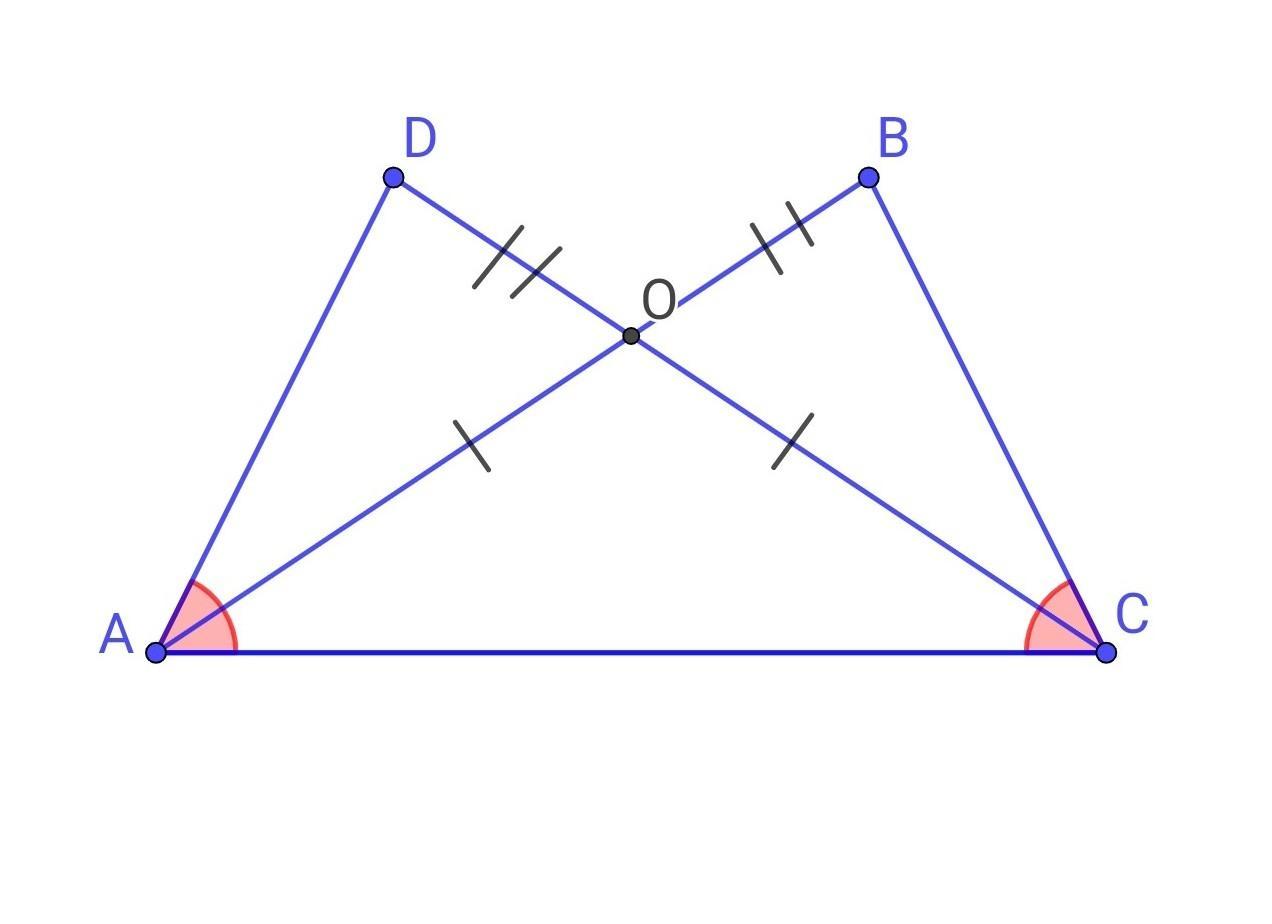
Дано: AO=OC, OD=OB
Довести: ∠DAC=∠BCA
Доведення
1. Розглянемо △AOD і △COB.
- AO=OC (умова)
- OD=OB (умова)
- ∠AOD=∠COB (як вертикальні)
△AOD=△COB за першою ознакою рівності трикутників (за двома сторонами і кутом між ними)
Отже AD=CB - як відповідні сторони рівних трикутників.
2. Розглянемо △ADC і △ CBA.
За аксиомою вимірювання відрізків отримаємо:
Отже:
- AB=DC
- AD=CB (п.1)
- АС - спільна
△ADC=△CBA за ||| ознакою рівності трикутників (за трьома сторонами).
Звідси маємо: ∠DAC =∠BCA.
Доведено.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
