Помогите пожалуйста, очень срочно!!! Даю 100 баллов
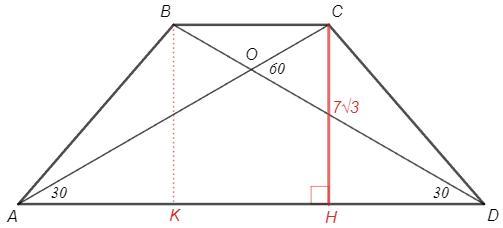
Висота рівнобічної трапеції дорівнює 7√3 см. Знайдіть площу трапеції, якщо кут між її діагоналями, протилежний бічній стороні трапеції, дорівнює 60°.
Ответы
Ответ:
S=147√3
Объяснение:
В равнобедренной трапеции углы при основании равны.
△BAD=△CDA по двум сторонам и углу между ними.
∠BDA=∠CAD
Внешний угол треугольника AOD равен 60, следовательно
∠OAD=∠ODA =60/2=30
Треугольник ACH с углами 30-60-90, стороны относятся 1:√3:2
----------------------------------------------------------------------------------------
Катет против угла 30 равен половине гипотенузы.
Пусть катет 1, гипотенуза 2
По т Пифагора другой катет =√(4-1) =√3
В треугольнике с углами 30-90 стороны относятся 1:√3:2
----------------------------------------------------------------------------------------
AH =CH*√3 =7√3*√3 =21
Докажем, что отрезок AH равен средней линии трапеции.
Опустим высоту BK.
KH=BC
△ABK=△DCH по гипотенузе и острому углу.
AK=HD =(AD-KH)/2 =(AD-BC)/2
Тогда AH =(AD+BC)/2
Площадь трапеции = AH*CH =21*7√3 =147√3