Question

Ma і MB дотичні до кола кут AMB=50 BD діаметр.Знайти кути трикутника DAO

Answer 1

Ответ:

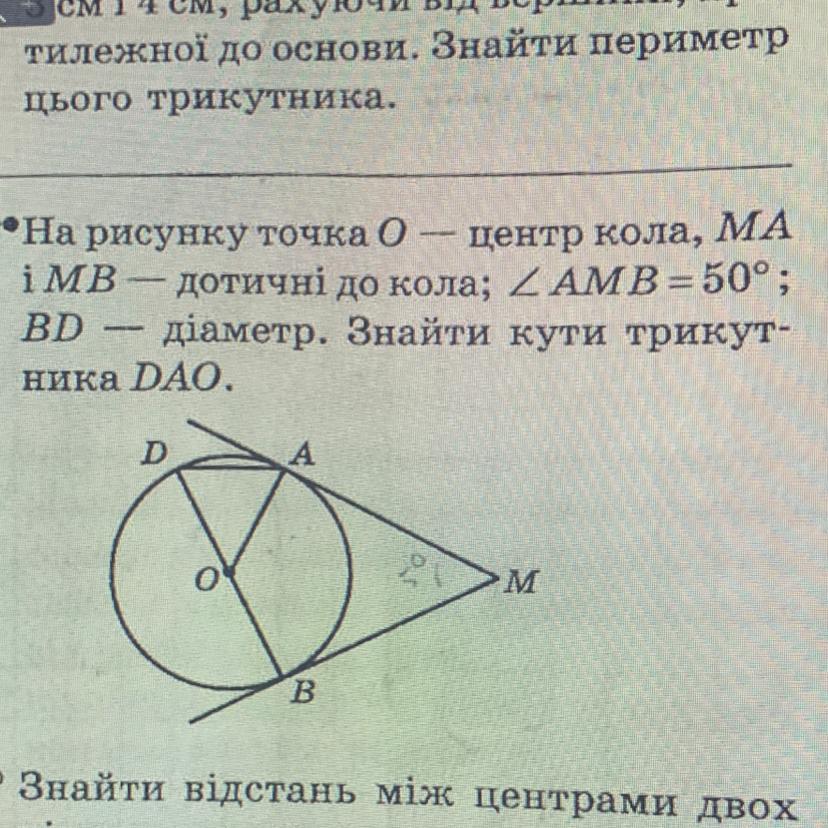
Углы треугольника DAO равны 65°, 65°, 50°.

Объяснение:

На рисунке точка О-центр окружности. МА и MB - касательные к окружности; ∠AМB = 50°; BD - диаметр. Найти углы треугольника DAO.

Дано: Окр.О;

МА и MB - касательные;

∠AМB = 50°;

BD - диаметр.

Найти: углы ΔDAO.

Решение:

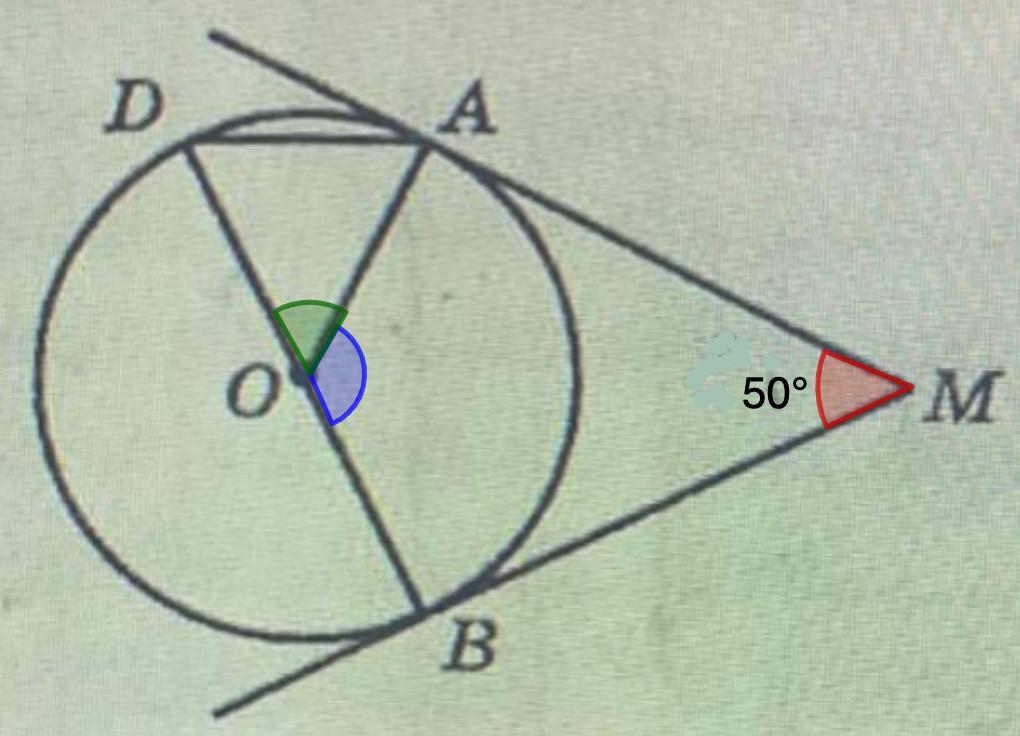
МА и MB - касательные; ∠AМB = 50°;

• Угол между двумя касательными, проведёнными из одной точки, равен 180° минус величина заключённой внутри него дуги.

⇒ ∠АМВ = 180° - ◡АВ

◡АВ = 180° - 50° = 130°

• Центральный угол равен градусной мере дуге, на которую он опирается.

⇒ ∠АОВ = ◡АВ = 130°

Рассмотрим ΔDAO.

OD = OA = R

⇒ ΔDAO - равнобедренный.

• Сумма смежных углов равна 180°.

⇒ ∠DOA = 180° -  ∠АОВ  = 180° - 130° = 50°

• Сумма углов треугольника равна 180°.

⇒ ∠ODA + ∠OAD = 180° - ∠DOA = 180° - 50° = 130°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠ODA = ∠OAD = 130° : 2 = 65°