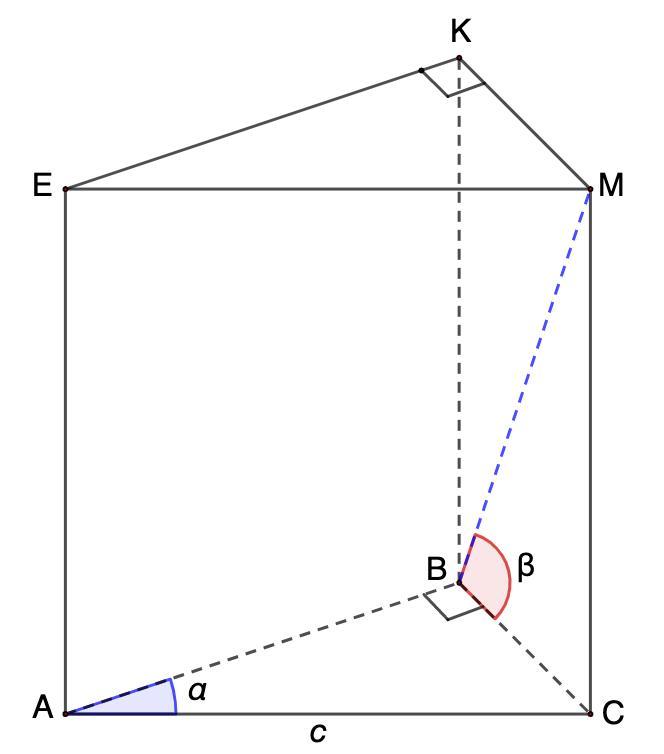
Основа прямої призми прямокутний трикутник з гіпотенузою с і гострим кутом а. Знайти об'єм призми, якщо діагональ бічної грані, що містить катет, протилежний куту а, утворює з площиною основи кут В.
Ответы
Ответ дал:
4
Ответ:
Объем призмы равен
Пошаговое объяснение:
Основание прямой призмы прямоугольный треугольник с гипотенузой с и острым углом α. Найти объем призмы, если диагональ боковой грани, содержащей катет, противоположный углу α, образует с плоскостью основания угол β.
Дано: АВСЕКМ - прямая призма;
ΔАВС - прямоугольный; АС = с; ∠ВАС = α
∠МВС = β;
Найти: V призмы.
Решение:
- Объем призмы равен:
V = Sосн. · h,
где h - высота призмы.
1. Найдем площадь основания.
- Площадь прямоугольного треугольника равна половине произведения катетов.
АС = с; ∠ВАС = α
- Синус угла - отношение противолежащего катета к гипотенузе.
- Косинус угла - отношение прилежащего катета к гипотенузе.
⇒ площадь основания равна:
2. Найдем высоту призмы.
Рассмотрим ΔВМС - прямоугольный.
- Тангенс угла - отношение противолежащего катета к прилежащему.
3. Найдем объем.
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад