Помогите пж (x-a)(2x-1)(x+b) 0 наидите числа а и в если решением неравенства явлется промежуток (-8;0,5) (10;+∞)
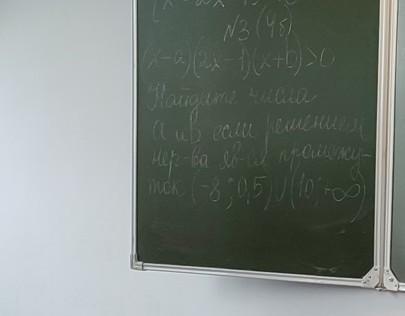
Ответы
Ответ:
a = -9 и b = 9.
Объяснение:
Чтобы найти числа a и b в выражении (x-a)(2x-1)(x+b), зная, что решением неравенства является промежуток (-8;0,5) и (10;+∞), мы можем использовать следующий подход:
Рассмотрим каждый из трех множителей в выражении и определим, какие значения переменных x соответствуют заданным промежуткам.
(x-a) должно быть положительным для x из промежутка (-8; 0,5). Это означает, что a должно быть меньше -8 и больше 0,5.
(2x-1) должно быть положительным для x из промежутка (-8; 0,5). Это означает, что (2x-1) должно быть больше 0 при подстановке значений из этого промежутка.
(x+b) должно быть положительным для x из промежутка (10; +∞). Это означает, что b должно быть меньше 10, чтобы (x+b) было положительным для всех x больше 10.
Теперь, когда мы знаем условия для a и b, можем перейти к поиску чисел a и b, удовлетворяющих этим условиям.
Из условия a < -8 и a > 0,5 можно заключить, что a не может быть определено однозначно. Мы можем выбрать, например, a = -9 и a = 1.
Из условия b < 10, мы можем выбрать, например, b = 9.
Таким образом, одним из возможных решений является a = -9 и b = 9.
вроде верно