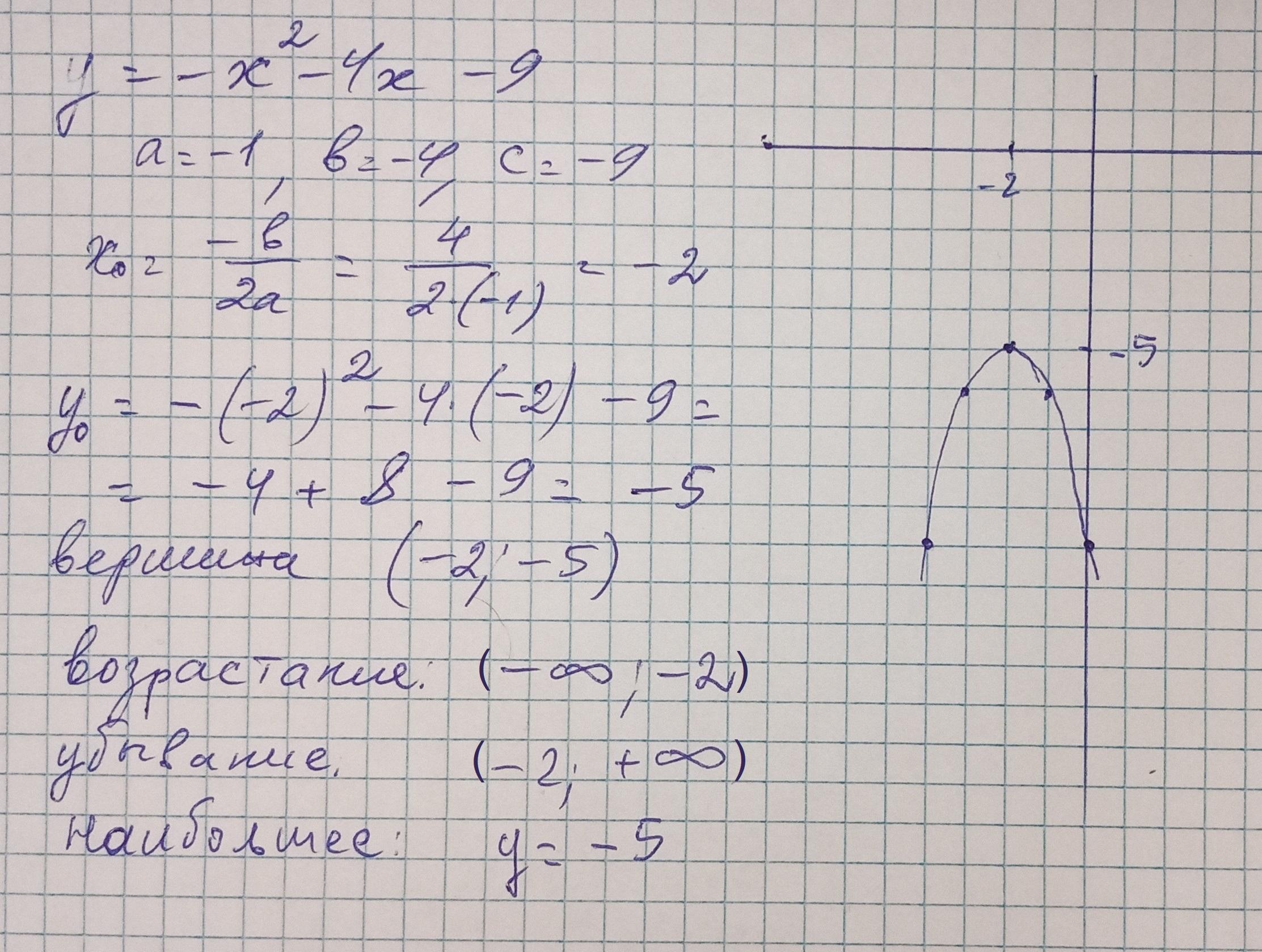Знайти проміжки зростання і спадання функцій y= - x² - 4x - 9 , та її найбільше значення
Ответы
Ответ:
Для знаходження проміжків зростання і спадання функції y = -x² - 4x - 9, спочатку потрібно знайти її першу похідну.
Похідна функції y = -x² - 4x - 9:
y' = -2x - 4
Далі, встановимо рівняння для знаходження критичних точок функції, де її похідна дорівнює нулю:
-2x - 4 = 0
Розв'язавши рівняння, отримаємо:
-2x = 4
x = -2
Отже, функція має критичну точку при x = -2.
Далі, розглянемо інтервали між цією критичною точкою та безкінечністю.
Інтервал перед критичною точкою (від -∞ до -2):
Виберемо довільну точку x₁ з цього інтервалу, наприклад, x₁ = -3.
Підставимо x₁ у початкову функцію:
y₁ = -(-3)² - 4(-3) - 9
y₁ = -9 + 12 - 9
y₁ = -6
Інтервал після критичної точки (від -2 до +∞):
Виберемо довільну точку x₂ з цього інтервалу, наприклад, x₂ = 0.
Підставимо x₂ у початкову функцію:
y₂ = -(0)² - 4(0) - 9
y₂ = -9
Таким чином, функція зростає на інтервалі (-∞, -2) та спадає на інтервалі (-2, +∞).
Найбільше значення функції можна знайти шляхом знаходження її вершини. Для цього можна використати формулу вершини параболи: x = -b / (2a), де a, b та c - коефіцієнти в рівнянні.
У даному випадку, a = -1, b = -4, c = -9. Підставляємо їх у формулу:
x = -(-4) / (2 * -1)
x = 2 / -2
x = -1
Знаходимо значення y в цій точці:
y = -(-1)² - 4(-1) - 9
y = -1 + 4 - 9
y = -6
Таким чином, найбільше значення функції становить -6.
Объяснение:
x = 4 /( -2)
x = -2
Ответ:
решение на фото
Объяснение: