Question

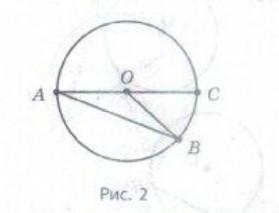
На рис. 2 точка О центр кола. Знайдіть:
1) кути трикутника АОВ, якщо ∠COB=30°;
2) кут COB, якщо кут OAB на 15° менший від кута АОВ. ​

Answer 1

Відповідь:

1) 15°, 15°, 150°.

2) 110°.

Пояснення:

1)

ΔAOB - рівнобедрений за двома сторонами (OA = OB = r), тож ∠А = ∠В.

За властивістю зовнішнього кута маємо, що ∠A + ∠B = ∠COB, тож ∠А = ∠В = 30° * 1/2 = 15°.

∠АОВ = 180° - ∠СОВ (суміжні кути) = 180° - 30° = 150°.

2)

ΔAOB - рівнобедрений за двома сторонами (OA = OB = r), тож ∠А = ∠В.

Тепер складемо рівняння, де ∠А = ∠В = x, ∠AOB = x + 15°.

x + x + x + 15° = 180°

3x = 165°

x = 55°

За властивістю зовнішнього кута маємо, що ∠A + ∠B = ∠COB, тож ∠СОВ = ∠А + ∠В = 55° + 55° = 110°.