Question

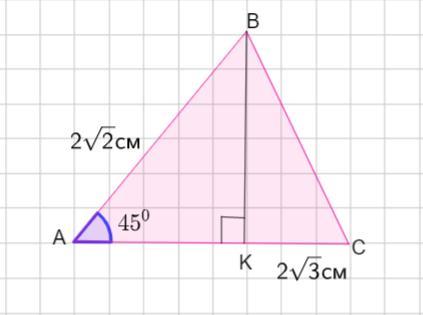
У трикутнику АВС відрізок ВК - висота. АВ = 2√2 см, КС = 2√3 см, ∠ВАК = 45. Знайти довжину сторони ВС

Answer 1

Ответ:

ВС = 4см

Объяснение:

В треугольнике АВС ВК - высота. АВ =2√2 см, КС =2√3 см, ∠ВАК=45°. Найти длину стороны ВС.

Пусть дан ΔАВС. ВК - высота .

Рассмотрим ΔАКВ - прямоугольный.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе .

$sin45^{0} =\dfrac{BK}{AB} ;\\\\\dfrac{\sqrt{2} }{2} =\dfrac{BK}{2\sqrt{2} } ;\\\\BK= \dfrac{2\sqrt{2} \cdot \sqrt{2} }{2} =2$ см.

Рассмотрим ΔВКС - прямоугольный.

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

ВС²= ВК² + КС²;

ВС² = 2²+ (2√3)²= 4 + 12 = 16;

ВС = √16 = 4 см.

#SPJ1