Ответы
Ответ дал:
0
Ответ:
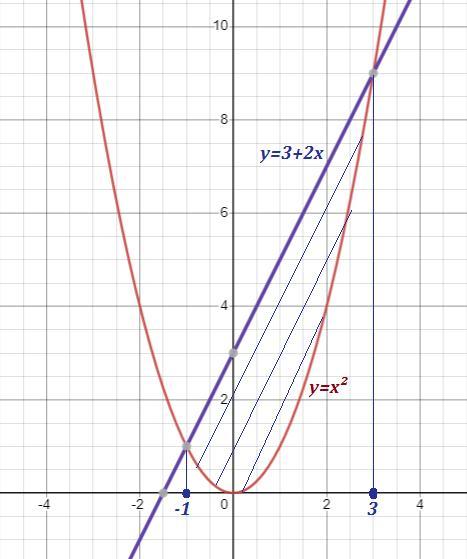
Найти площадь области, ограниченной линиями
Точки пересечения : .
По теореме Виета находим .
Приложения:

Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад