Звести рівняння кривої до нормального вигляду та побудувати її графік
Завдання записати в зошиті з повним розв’язком і малюнком. Дякую!
Приложения:
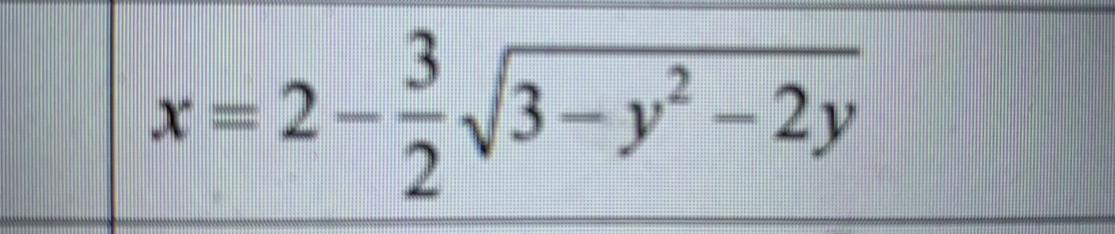
Ответы
Ответ дал:
1
Ответ:
Уравнение кривой имеет вид
Возведём в квадрат обе части равенства .
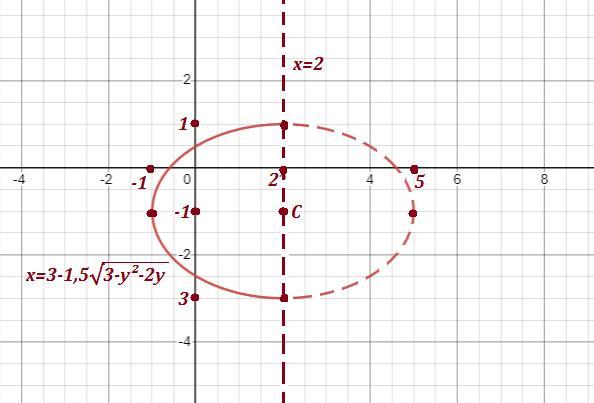
Получили , что заданной кривой является половина эллипса, которая расположена левее прямой х=2 . Эта половина на чертеже нарисована сплошной линией .
Центр эллипса находится в точке C( 2 ; -1 ) . Большая полуось равна а=3 , малая полуось равна b=2 .
Приложения:

Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад