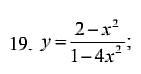Question

Дослідити функцію та побудувати її графік:

Answer 1

Исследуйте функцию и постройте ее график

$f(x) = \dfrac{2-x^2}{1-4x^2}$

1.Область определения :

По определению знаменатель не может быть равен нулю

1 - 4x² ≠ 0

(1-2x)(1+2x) ≠ 0 ⇒

$D(y) =\left \{ \begin{array}{l}x\neq -0,5 \\ x\neq 0,5 \end{array}$    или  $x \in (-\infty ~ ; ~ -0,5)\cup (~-0,5~;~0,5 ~)\cup (0,5 ~ ; ~ \infty )$

2.Четность , нечетность :

$f(-x) = \dfrac{2-(-x)^2}{1-4(-x)^2} = \dfrac{2-x^2}{1-4x^2} = f(x)$  ⇒  функция является четной

3.Пересечение с осями координат :

Ox ⇒ y = 0

$\displaystyle \dfrac{2-x^2}{1-4x^2} = 0 \\\\ 2-x^2 = 0 \\\\ x_1 = \sqrt{2 } ~~ , ~~ x_2 =-\sqrt{2}$

Oy ⇒ x = 0

$\displaystyle \dfrac{2-0^2}{1-4\cdot 0^2} = 2$

4.Непрерывность :

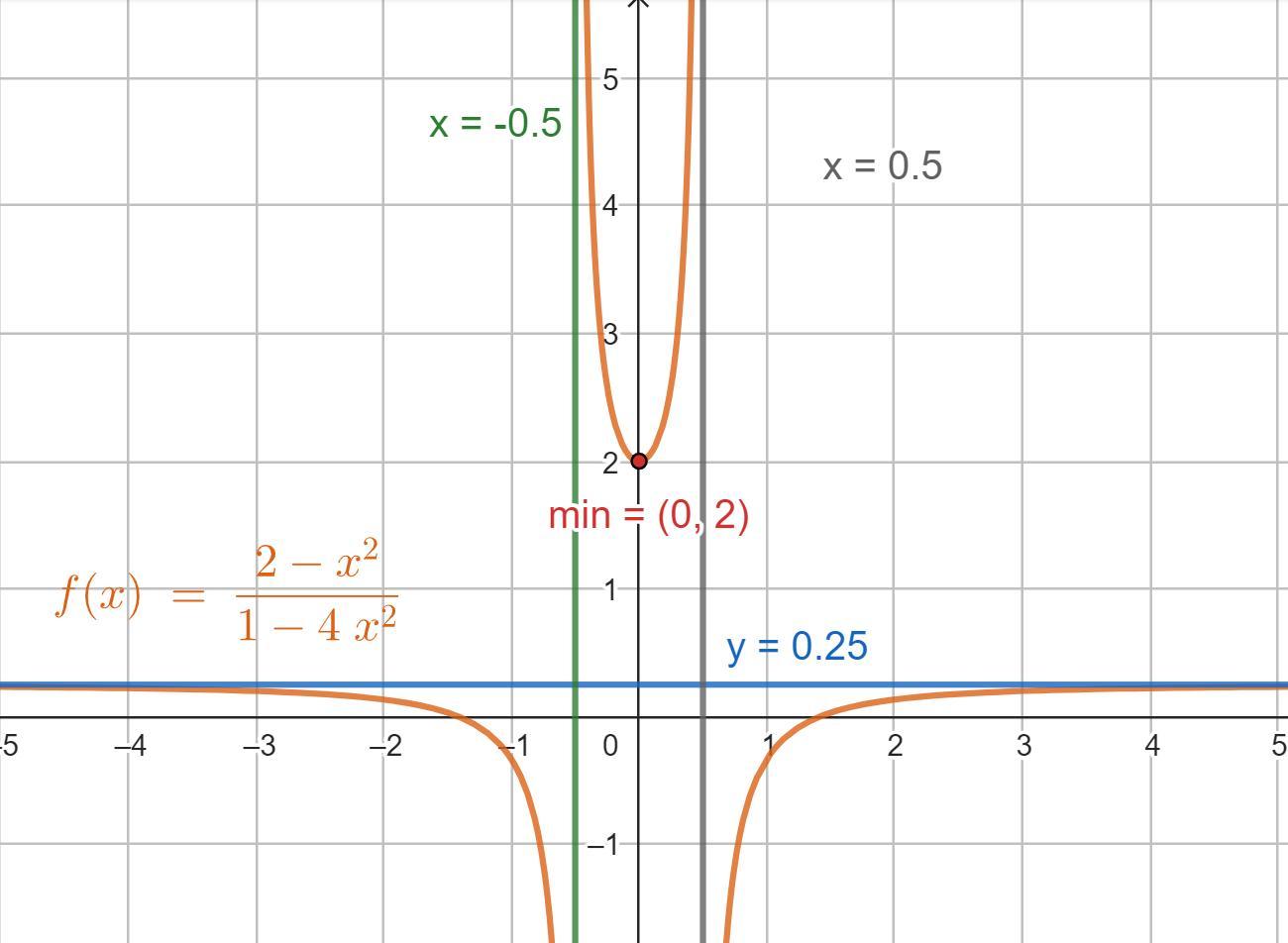
x = 0,5  ;  x =-0,5   —  вертикальные асимптоты

Найдем наклонную асимптоту

$y = kx + b \\\\\displaystyle k = \lim_{x \to \pm\infty} \frac{f(x)}{x} ~ ; ~b = \lim_{x \to \pm\infty}\big(f(x)-kx \big )$

$\displaystyle k = \lim_{x \to \pm \infty} \frac{2-x^2}{x(1-4x^2)} = \lim_{x \to \pm \infty}\frac{\dfrac{2}{x^2} - \dfrac{x^2}{x^2} }{\dfrac{x}{x^2} - \dfrac{4x^3}{x^2} } = \frac{\dfrac{2}{\infty ^2} -1 }{0 - 4\cdot (\pm \infty ) } = \frac{-1}{4\cdot \mp \infty } = 0$

$\displaystyle b = \lim_{x \to \pm\infty}\bigg( \frac{2-x^2}{1-4x^2} -0\cdot x \bigg )= \lim_{x \to \pm\infty}\ \frac{\dfrac{2}{x^2} -1}{\dfrac{1}{x^2} - 4 } = \frac{1}{4}$

⇒  мы получили горизонтальную асимптоту  y = 0,25

5.Возрастание , убывание , экстремумы :

$\displaystyle f'(x) =\bigg ( \dfrac{2-x^2}{1-4x^2} \bigg )' = \frac{(2-x^2)'(1-4x^2) - (2-x^2)(1-4x^2)'}{(1-4x^2)^2} = \\\\\\ =\frac{-2x (1-4x^2) -(2-x^2) \cdot (-8x)}{(1-4x^2)^2} =\frac{-2x + 8x^3 + 16x-8x^3}{(1-4x^2)^2} = \\\\\\ =\frac{14x }{(1-2x)^2(1+2x)^2}$

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(.3 ,-.2){ \Large \Large \searrow } \put(0.85,-0.3) {\sf -0,5}  \put(1.36 ,-.2){ \Large  \Large \searrow } \put(1.29 ,0.1){ \Large  \LARGE  \text{ ---} }    \put(.25 ,0.1){ \LARGE  \text{ ---} } \put(2.35 ,0.1){ \Large+ }          \put(3.3 ,0.1){ \Large+ }       \put(1,0){\circle{0.055}}   \put(2.01,-0.3) {\sf 0}\put(2.05,0){\circle*{0.055}}       \put(2.35 ,-.2){ \Large \nearrow }  \put(2.9,-0.3) {\sf 0,5}\put(3,0){\circle{0.055}}    \put(3.35 ,-.2){ \Large \Large \nearrow  } \put(0,0){\vector (1,0){4}}  \end{picture}$

$\Large \boldsymbol{ \nearrow }$ Возрастает когда $x\in[~0~ ; ~ 0,5 )~; ~ (~0,5~ ; ~ \infty ~]$

$\Large \boldsymbol{ \searrow }$ Убывает когда $x \in ( -\infty ~ ; - 0,5~) ~; ~ ( ~-0,5~; ~ 0 ~]$

Если производная меняет знак c «+» на «-» , то в данной точке будет максимум , если c «-» на «+», то минимум .

Поскольку на интервале закрашен только  0 ,  то  x min = 0

$y_{\min}= f(0) = \dfrac{2-0}{1-4\cdot 0^2} = 2$

6.Выпуклость вогнутость :

Найдем вторую производную

$\displaystyle f''(x) =\bigg ( \dfrac{14x }{(1-4x^2)^2} \bigg ) '= \frac{(14x)'\cdot (1-4x^2)^2+ 14x \cdot \Big( (1-4x^2)^2\Big)'}{(1-4x^2)^4} = \\\\\\ = \frac{14\cdot (1-4x^2)^2 - 14 x\cdot 2\cdot (1-4x^2)\cdot - 8x}{(1-4x^2)^2} = \\\\\\=\frac{14(1-4x^2) \Big( 1-4x^2 +16x^2 \Big)}{(1-4x^2)^4} = \frac{14(12x^2 +1)}{(1-2x)^3(1+2x)^3}$

Поскольку числитель не может быть равен нулю , то данная функция не будет иметь точек перегиба
Рассмотрев   знаменатель получим интервал

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(.85,-0.3) {\sf -0.5} \put(.2 ,0.1){ \Large \text{ +} } \put(.17 ,-0.3){ \Huge \smile } \put(1.3 ,0.1){ \LARGE ---} \put(1.27 ,-0.3){ \Huge \frown } \put(2.25 ,0.1){ \Large \text{ +} } \put(1,0){\circle{0.055}} \put(2.25 ,-0.3){ \Huge \smile } \put(1.95,-0.3) {\sf 0,5}\put(2.05,0){\circle{0.055}} \put(1,0.3) \ \put(0,0){\vector (1,0){3}} \end{picture}$

Если     « + »  , то функция  вогнута

Если     «—»  , то функция выпукла

Итак , если $x \in ( -\infty ~ ; -0,5 ) ~ ; ~ (0,5 ~ ; ~\infty)$  - функция  вогнута ,  если $x \in (-0,5 ~ ; ~ 0,5)$   - функция выпукла

7.График в приложенном файле

#SPJ1