Question

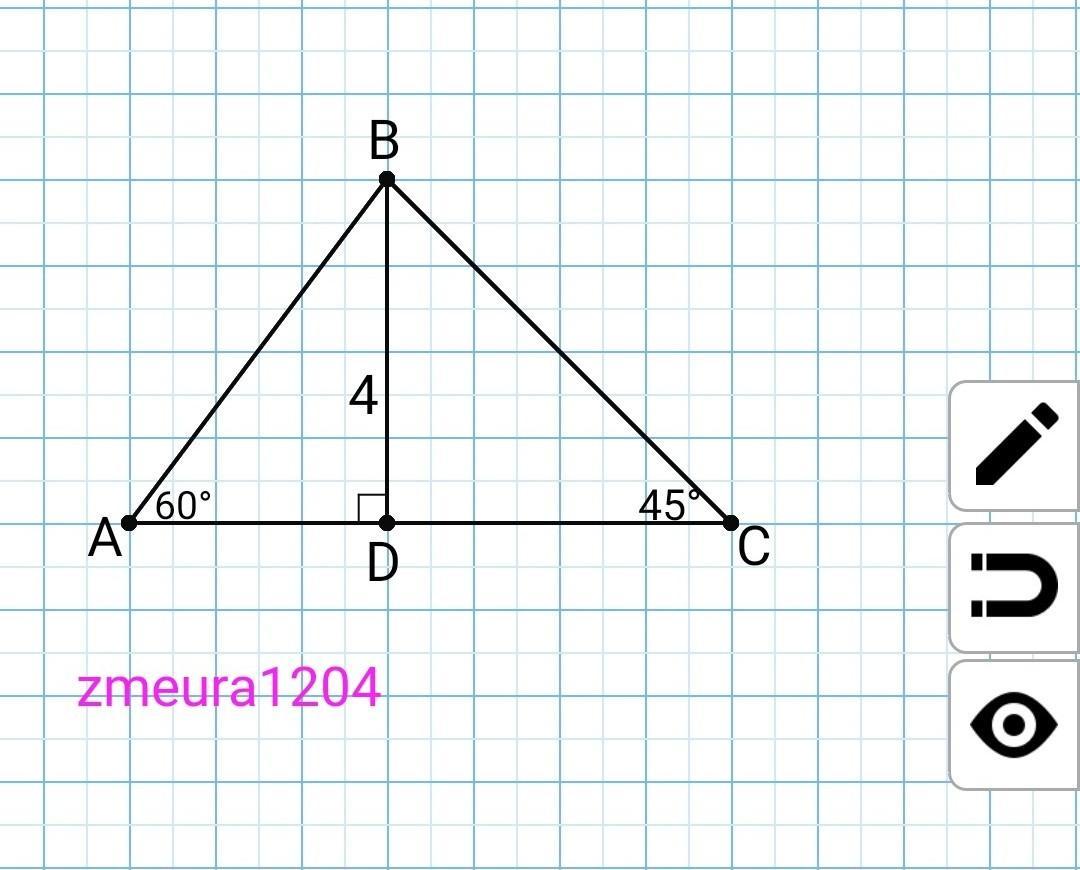
У трикутнику ABC ∠ A = 60°, ∠ C = 45°, BD = 4 см — висота трикутника. Знайдіть довжини сторін AB і BC, периметр та площу

Answer 1

Ответ:

Периметр трикутника дорівнює (4√3+4√2+4)см

Площа трикутника дорівнює (8√3+24)/3см²

Объяснение:

∆ABD- прямокутний трикутник.

∠ВDA=90°; ∠A=60°;

∠ABD=90°-∠A=90°-60°=30°

AD- катет проти кута 30°, в два рази більше гіпотенузи АВ=2*АD;

АD=x; AB=2x.

Теорема Піфагора:

ВD=√(AB²-AD²)=√((2x)²-x²)=

=√(4x²-x²)=x√3.

BD=x√3; BD=4см

х√3=4

х=4/√3=4√3/3 см АD.

AB=2*AD=2*4√3/3=8√3/3см

∆ВDC- прямокутний, рівнобедрений трикутник

Кути при основі рівні по 45°

ВD=DC=4см.

Теорема Піфагора:

ВС=√(ВD²+DC²)=√(4²+4²)=

=4√2см.

АС=АD+DC=4√3/3+4=

=4√3/3+4*3/3=(4√3+12)/3см

Р(∆АВС)=АВ+ВС+АС=

=8√3/3+4√2+(4√3+12)/3=

=8√3/3+12√2/3+(4√3+12)/3=

=(8√3+12√2+4√3+12)/3=

=(12√3+12√2+12)/3=

=4√3+4√2+4≈16,6 см.

S=½*BD*AC=½*4*(4√3+12)/3=

=2(4√3+12)/3=(8√3+24)/3 см²