Question

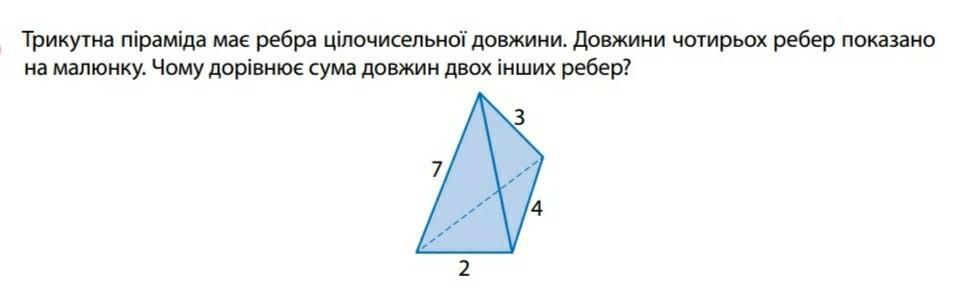
Треугольная пирамида имеет ребра целочисленных длин. Длины четырех ребер показано на рисунке. Чему равна сумма длин двух других ребер? ​

Answer 1

Ответ: 5+6=11

Объяснение:

Для решения данной задачи воспользуемся неравенством треугольника. Рассмотрим треугольник- основание пирамиды.

1 Сторона =2 , вторая 4. 3-я (назовем ее х) не может быть равна 2 и меньше так как х+2>4 => x может быть =3 .

Но она же является стороной грани - треугольник со сторонами 7 и 3

То есть должно выполняться неравенство 3+х>7

Поэтому 3 и 4 не годятся.

Годится для обоих треугольников х=5 .  Основание 2+4>5

боковая грань: 3+5>7 . Но 6 и больше не годятся для основания.

Поскольку 2+4>6 - неверное равенство.

Теперь назовем неизвестное ребро передней грани у

Должно выполняться неравенство 2+y>7 => y>5

Но рассмотрев боковую грань справа запишем  3+4>y

=>  5<y<7 => y=6

Сумма найденных ребер 5+6=11