Question

У прямокутному трикутнику АВС ( /С = 90°) провели висоту СD. Доведіть, що бісектриси кутів АВС і АСD перпендикулярні.

Answer 1

Ответ:

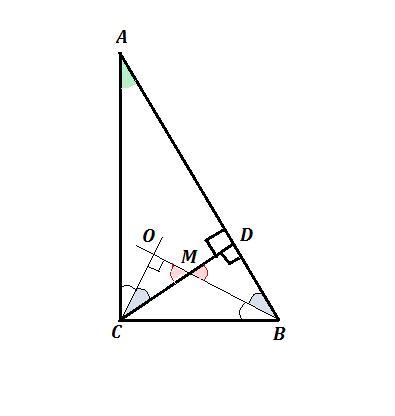
ΔАВС - прямоугольный , ∠С=90° ,  СD ⊥ AB , ВО - биссектриса ∠АВС ,  СО - биссектриса ∠АСD  . Доказать, что ВО ⊥ СО .

ΔАСD и ΔАBC - прямоугольные подобные треугольники .

У них есть общий угол А  и углы по 90° , тогда  ∠АСD=∠АВС .

Отсюда и половинки этих углов будут равны : ∠ОСD = ∠OBD .

Рассмотрим ΔОСМ и ΔDBM .

В этих треугольниках ∠ОМС = ∠DMB как вертикальные , а также

∠ОСМ = ∠DBM ( было доказано выше).

Значит и третьи углы будут равны,  ∠СОM = ∠ВDM .

Но ∠BDM = 90° по условию.

Значит ,  ∠СОМ = 90°  . А это угол - угол между биссектрисами  ВО

и СО .  Поэтому  ВО ⊥ СО .