Question

Розвʼязати задачу (Тема: Задачі на побудову)
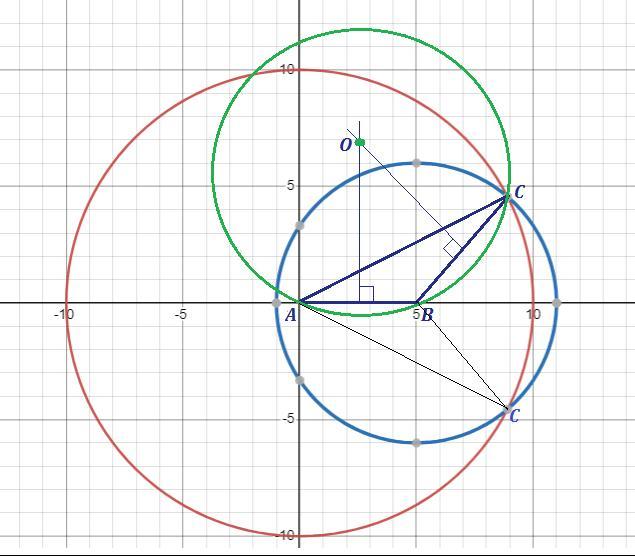
Побудуй трикутник АВС зі сторонами АВ-5 см, ВС-6 см, АС-10 см й опиши навколо нього коло. Знайди радіус описаного кола.

Answer 1

Ответ:

Стороны треугольника равны АВ=5 см , ВС=6 см , АС=10 см .

Такой треугольник существует, так как выполняется неравенство треугольника :  5+6>10  ,  5+10>5  ,  6+10>5  .

Cначала проведём прямую. На ней от выбранной точки А отложим отрезок  АВ  и отметим другой конец отрезка, точку В .  Затем проведём окружность с центром в очке А и радиусом, равным  АС . Потом проведём окружность с центром в очке В и радиусом, равным  ВС .  Точка пересечения окружностей является третьей вершиной треугольника С .

Центр окружности, описанной около треугольника лежит на пересечении серединных перпендикуляров к сторонам треугольника . Радиус описанной окружности можно найти по формуле

$\bf R=\dfrac{abc}{4S}$

Площадь треугольника можно найти по формуле Герона .

$\bf S=\sqrt{p(p-a)(p-b)(p-c)}$   .

$\bf p=\dfrac{1}{2}\cdot (5+6+10)=\dfrac{1}{2}\cdot 21=10,5\\\\\\S=\sqrt{\dfrac{21}{2}\cdot \Big(\dfrac{21}{2}-5\Big)\Big(\dfrac{21}{2}-6\Big)\Big(\dfrac{21}{2}-10\Big)}=\sqrt{\dfrac{21}{2}\cdot \dfrac{11}{2}\cdot \dfrac{9}{2}\cdot \dfrac{1}{2}}=\\\\\\=\dfrac{3}{4}\sqrt{21\cdot 11}=\dfrac{3}{4}\sqrt{231}$  

Теперь найдём радиус описанной окружности .

$\bf R=\dfrac{abc}{4S}=\dfrac{5\cdot 6\cdot 10}{3\sqrt{231}}=\dfrac{100}{\sqrt{231}}=\dfrac{100\sqrt{231}}{231}$    (см) .