У прямокутного трикутника сторона АС дорівнює 150 см. кут С дрівнює 15 градусів. Знайдіть дві інші сторони цього трикутника, СРОЧНО. ДАЮ 40 БАЛІВ. ДУЖЕ ТРЕБА
Приложения:

Ответы
Ответ дал:
0
Ответ:
на фото
Объяснение:
на фото
ххххххххх
Приложения:
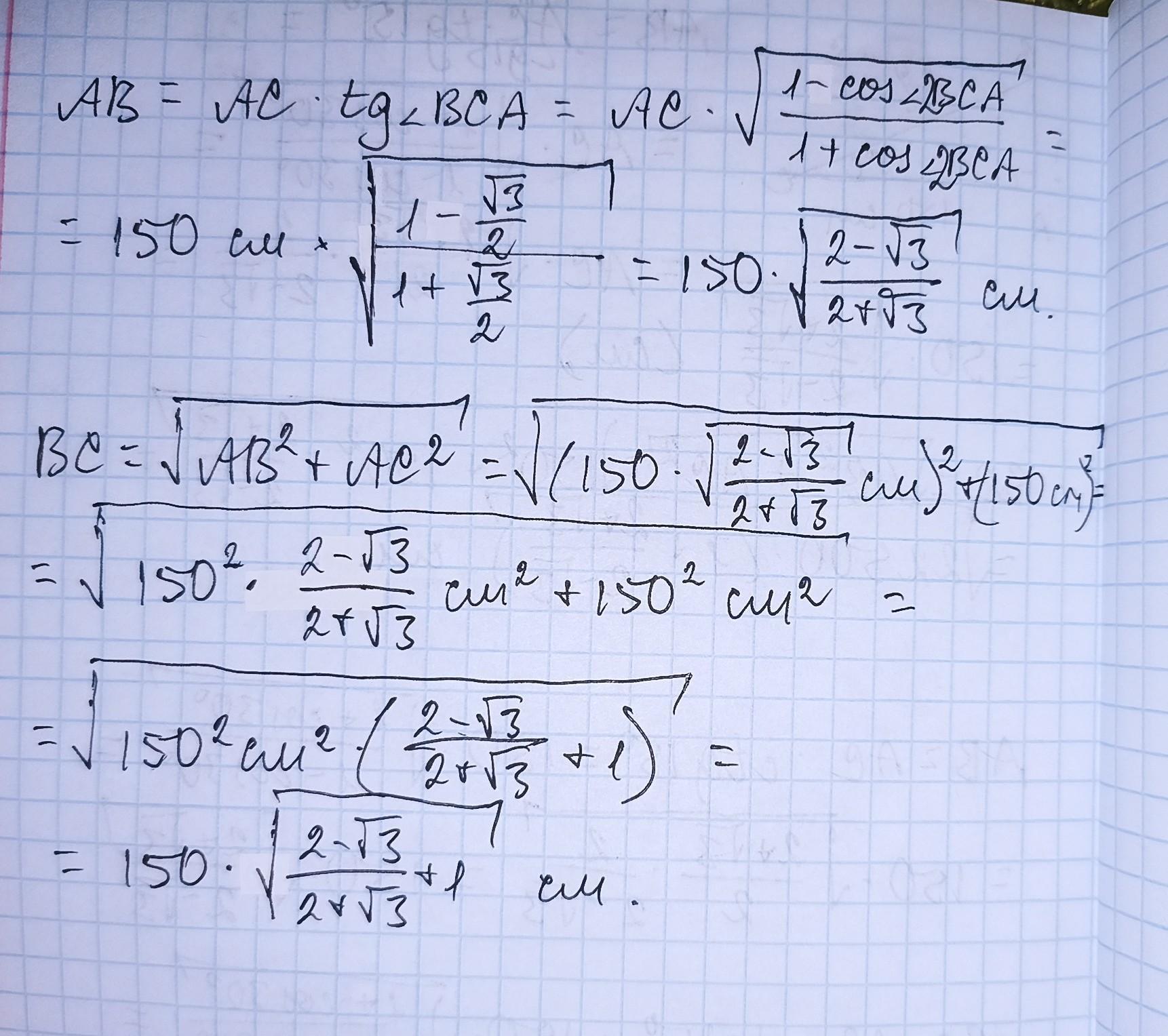
Ответ дал:
0
Ответ:
ΔABC - прямоугольный , ∠А=90° , ∠С=15° , АС=150 см .
Найдём тригонометрические функции угла в 15° .
(см)
Приложения:

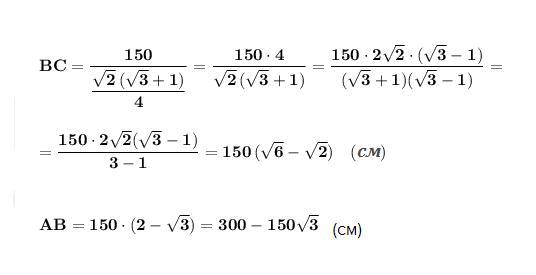
Вас заинтересует
1 год назад
3 года назад
3 года назад
8 лет назад