Найдите площадь фигуры, образованного при помощи соединения точек с координатами
A (5:8), B (1;0) и C (10:4)
Ответы
Ответ дал:
0
Ответ:
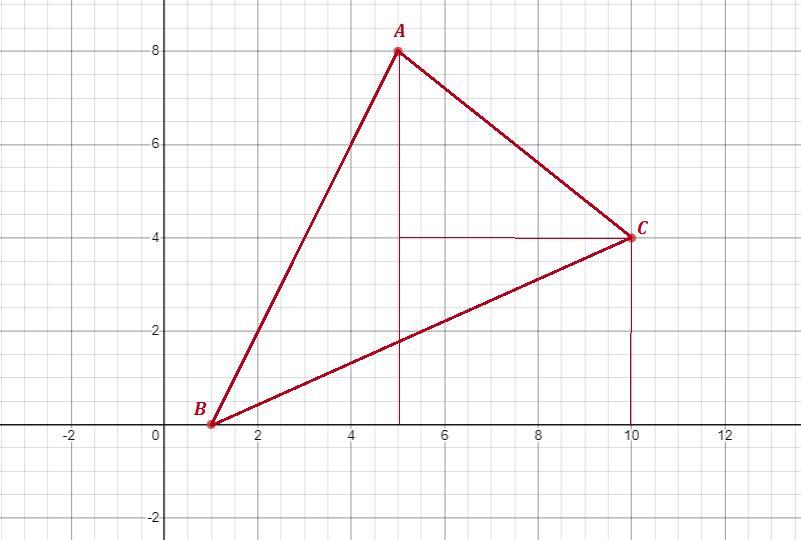
Соединив точки А(5;8) , В(1;0) , С(10;4) .
Легко найти длины сторон и применить формулу Герона для нахождения площади треугольника .
Полупериметр равен .
Вычислим произведение :
Вычислим площадь треугольника .
Приложения:

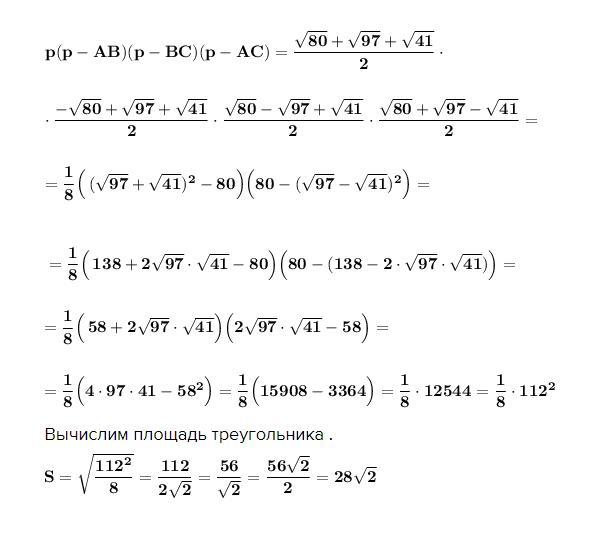
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад