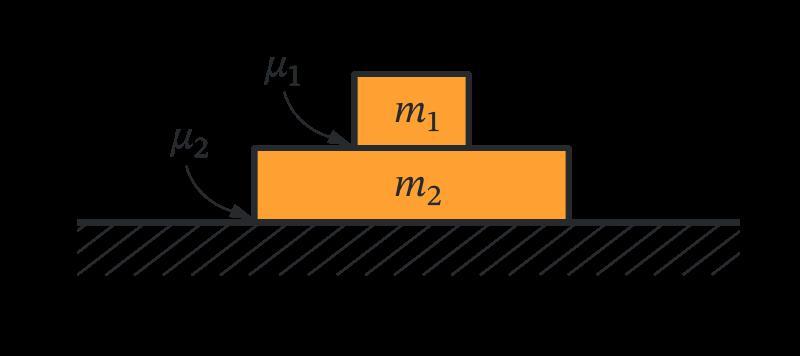
Два бруска лежат друг на друге, как показано на рисунке.
Отношение масс брусков m2/m1=2, отношение коэффициентов трения между брусками μ1 и между нижним бруском и горизонтальной поверхностью стола μ2 равно μ1/μ2=2.
Известно, что система выйдет из состояния равновесия, если к нижнему бруску приложить горизонтальную силу не менее F1 = 7,8Н. А какую минимальную горизонтальную силу нужно прикладывать к верхнему бруску, чтобы система вышла из положения равновесия? Ответ дайте в Н, округлив до десятых.
Ответы
Ответ: Искомая сила = 5,2 Н.
Объяснение: Выразим массы брусков и коэффициенты трения из заданного условия.
Дано:
m1 = m
m2 = 2m
μ2 = μ
μ1 = 2μ
Найти какую минимальную горизонтальную силу нужно прикладывать к верхнему бруску, чтобы система вышла из положения равновесия
F2 - ?
Максимальная сила трения между нижним бруском и поверхностью стола, с одной стороны по условию = F1 = 7,8Н, с другой стороны эта сила определяется выражением: F1 = (m1 + m2)*g*μ2. С учетом принятых обозначений F1 = (m + 2m)g*μ = 3m*g*μ.
Максимальная сила трения между брусками F = m1*g*μ1, с учетом принятых обозначений F = 2m*g*μ.
Как видим эта сила трения меньше F1, следовательно, при действии этой силы на верхний брусок верхний брусок сместится, а нижний останется в покое. Таким образом, эта сила будет являться минимальной для выведения системы из равновесия. Величину этой силы найдем разделив F1 на F. Имеем: F1/F = 3m*g*μ/2m*g*μ. = 3/2. Отсюда искомая сила F2 = F1/(3/2) = 7,8/1,5 = 5,2 Н.