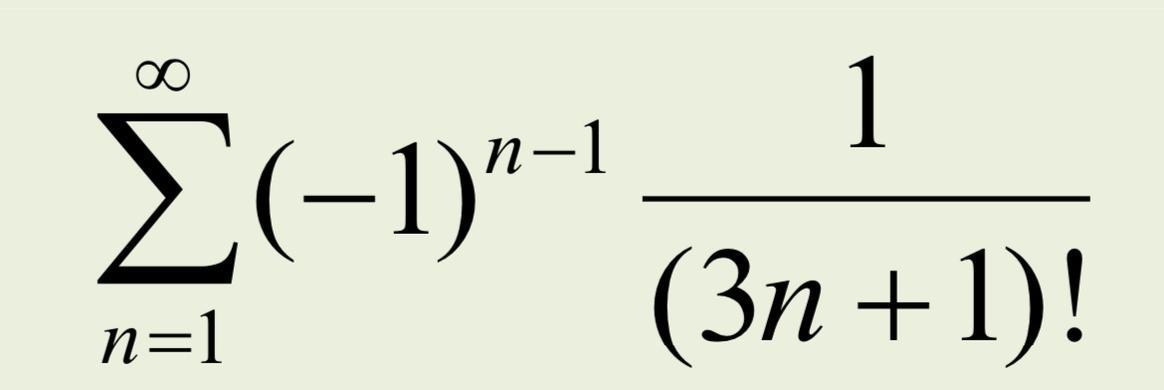Ответы
Ответ дал:
1
Согласно первому признаку Лейбница, каждый последующий член ряда в абсолютной величине должен быть меньше предыдущего. В нашем случае этому условию удовлетворяет ряд:
1/24 > 1/5040 > 1/3628800 > ...
Согласно второму признаку Лейбница предел ряда должен стремиться к 0. В данной ситуации это условие также выполняется.
Согласно признаку Лейбница, ряд сходится. Теперь остается проанализировать его абсолютную и условную сходимость. Для этого возьмем абсолютное значение данного ряда.
- сходящийся по признаку Даламбера, так как
Следовательно, данный ряд сходится абсолютно
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад