Разложить функцию f (х) вокруг заданную точки ряд Тейлора или
Маклорена и найти область сходимости полученного ряда.
Приложения:
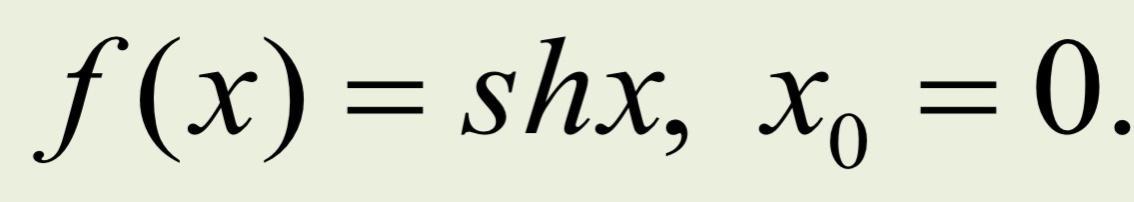
Ответы
Ответ дал:
0
Ответ:
Область сходимости
Объяснение:
Ряд Маклорена:
Найдем радиус области сходимости ряда (-R; R):
Значит, ряд сходится при любом значении x:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад