Ответы
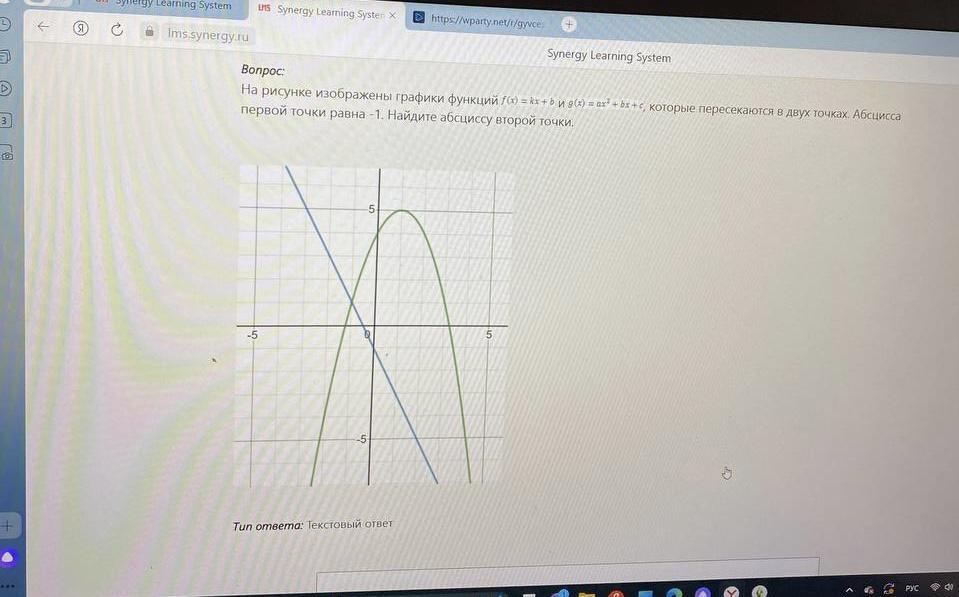
На рисунке изображены графики функций f(x)= kx+b и g(x)=ax²+ bc+c , которые пересекаются в двух точках. Абсцисса первой точки равна -1. Найдите абсциссу второй точки.
Пошаговое объяснение:
1)Уравнение параболы можно записать в другой форме
g(x)= a•(x - x₀)²+y₀ , где x₀, y₀— координаты вершины параболы.
На чертеже вершина имеет координаты (1;5).
Подставляем
g(x)= a•(x - 1)² +5 . По графику видно , что а=-1. Тогда g(x)= -1(x - 1)² +5 .
2)Прямая f(x)= kx+b проходит через точки
(-1; 1), {1=k*(-1)+b,
(0;-1) , {-1=k*0+b . ⇒b=-1.Тогда
1=-k -1 ⇒k=-2.
Тогда f(x)= -2x-1.
3)Графики пересекаются , значит
-1(x - 1)² +5=-2x-1,
-1(x²-2х+1)+5+2x+1=0,
x² -2х+1-5-2x-1=0,
x²-4х-5=0.
По теореме Виета х₁•х₂=-5 ,
-1•х₂ =-5 ⇒ х₂=5
Абсцисса второй точки 5.