Question

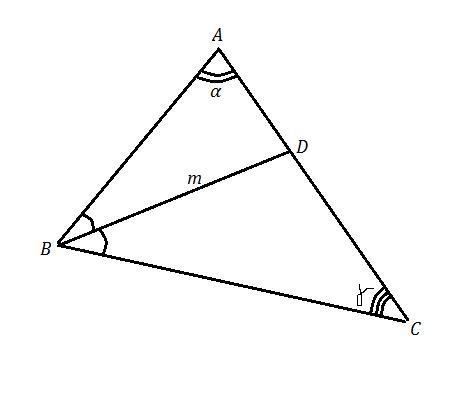
У трикутнику ABC провели бісектрису BD. Знайдіть сторони трикутника ABC, якщо BD = m, кут А = альфа, кут С = гамма.
Очень нужно подробное решение с объяснением. Спасибо

Answer 1

Решение .

ΔАВС , ВD - биссектриса  ⇒   ∠АВD = ∠CBD ,  

BD = m  ,  ∠A = α , ∠C = $\boldsymbol{\gamma}$  .  Найти :  АВ , ВС , АС .  

Сумма углов треугольника равна 180°   ⇒  ∠А + ∠В + ∠С = 180°  ,

$\boldsymbol{\alpha +\gamma +\angle B = 180^\circ \ \ \Rightarrow \ \ \ \angle B = 180^\circ -(\alpha +\gamma )}\\\\\boldsymbol{\angle {ABD}=\angle {CBD}=\dfrac{1}{2}\cdot \angle {B}=90^\circ -\dfrac{\alpha +\gamma }{2}}\\\\\boldsymbol{sin\angle {ABD}=sin\angle {CBD}=sin\Big(90^\circ -\dfrac{\alpha +\gamma }{2}\Big)=cos\dfrac{\alpha +\gamma }{2}}$      

Рассмотрим ΔABD . Найдём   ∠АDВ :

$\boldsymbol{\angle{ADB}=180^\circ -\alpha -\Big(90^\circ -\dfrac{\alpha +\gamma }{2}\Big)=90^\circ -\dfrac{\alpha }{2}+\dfrac{\gamma }{2}=90^\circ -\Big(\dfrac{\alpha -\gamma }{2}\Big)}$  

По теореме синусов :  $\boldsymbol{\dfrac{m}{sin\alpha }=\dfrac{AB}{sin\angle{ADB}}=\dfrac{AD}{sin\angle{ABD}}}$  ,  

$\boldsymbol{sin\angle{ADB}=sin\Big(90^\circ -\dfrac{\alpha -\gamma }{2}\Big)=cos\dfrac{\alpha -\gamma }{2}}$   .  

$\boldsymbol{AB=\dfrac{m\cdot sin\angle{ADB}}{sin\alpha }=\dfrac{m\cdot cos\dfrac{\alpha -\gamma }{2}}{sin\alpha }}$      

$\boldsymbol{AD=\dfrac{m\cdot sin\angle{ABD}}{sin\alpha }=\dfrac{m\cdot cos\dfrac{\alpha +\gamma }{2}}{sin\alpha }}$  

Рассмотрим  ΔСBD . Найдём  sin∠CDB .

$\boldsymbol{\angle{CDB}=180^\circ -\angle{ADB}=180^\circ -\Big(90^\circ -\dfrac{\alpha -\gamma }{2}}\Big)}=\boldsymbol{90^\circ +\dfrac{\alpha -\gamma }{2}\ \ ,}\\\\\boldsymbol{sin\angle{CDB}=sin\Big(90^\circ +\dfrac{\alpha -\gamma }{2}\Big)=cos\dfrac{\alpha -\gamma }{2}}$  

По теореме синусов :   $\boldsymbol{\dfrac{m}{sin\gamma }=\dfrac{BC}{sin\angle{CDB}}=\dfrac{CD}{sin\angle{CBD}}\ \ \ \Rightarrow }$  

$\boldsymbol{BC=\dfrac{m\cdot sin\angle{CDB}}{sin\gamma } =\dfrac{m\cdot cos\dfrac{\alpha -\gamma }{2}}{sin\gamma}\ \ ,}\\\\\boldsymbol{CD=\dfrac{m\cdot sin\angle{CBD}}{sin\gamma } =\dfrac{m\cdot cos\dfrac{\alpha +\gamma }{2}}{sin\gamma}\ \ .}$                

Найдём сторону AC : $\boldsymbol{AC=AD+CD=\dfrac{m\cdot cos\dfrac{\alpha +\gamma }{2}}{sin\alpha }+\dfrac{m\cdot cos\dfrac{\alpha +\gamma }{2}}{sin\gamma }}=\\\\\\\boldsymbol{=m\cdot cos\dfrac{\alpha +\gamma}{2}\cdot \Big(\dfrac{1}{sin\alpha }+\dfrac{1}{sin\gamma}\Big)=m\cdot cos\dfrac{\alpha +\gamma}{2}\cdot \dfrac{sin\alpha +sin\gamma }{sin\alpha \cdot sin\gamma }}$      

Ответ:  $\boldsymbol{AB=m\cdot cos\dfrac{\alpha -\gamma}{2}\cdot \dfrac{1}{sin\alpha }\ \ ,\ \ \ BC=m\cdot cos\dfrac{\alpha -\gamma}{2}\cdot \dfrac{1}{sin\gamma }\ \ ,}$  

             $\boldsymbol{AC=m\cdot cos\dfrac{\alpha +\gamma}{2}\cdot \dfrac{sin\alpha +sin\gamma }{sin\alpha \cdot sin\gamma }\ \ .}$