Question

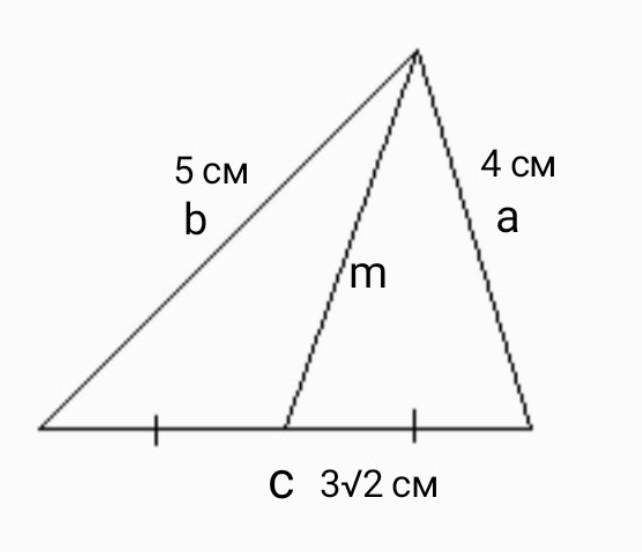
Стороны треугольника равны 4 см, 5 см и 3√2 см. Найдите длину медианы, проведенной к средней стороне.


Помогите, с подробным решением пожалуйста (желательно с иллюстрацией)

Answer 1

Ответ:

4 см.

Объяснение:

1) Медиану треугольник можно найти по формуле:

$m = \frac{1}{2} \sqrt{2 {a}^{2} + 2 {b}^{2} - {c}^{2} }$

где m - медиана, с - сторона, к которой эта медиана проведена, а и b - другие стороны треугольника. Данная формула является следствием из теоремы косинусов.

2) Проверим, какая сторона треугольника является средней. Для этого все стороны представим под корнем:

4 см = √16 см

5 см = √25 см

3√2 см = √9×2 см = √18 см

Значит средней является сторона с длиной 3√2 см.

Тогда а = 4 см, b = 5 см, с = 3√2 см.

Подставим эти значения в формулу:

$m = \frac{1}{2} \sqrt{2 \times {4}^{2} + 2 \times {5}^{2} - {(3 \sqrt{2)} }^{2} } = \frac{1}{2} \sqrt{2 \times 16 + 2 \times 25 - 18} = \frac{1}{2} \sqrt{32 + 50 - 18} = \frac{1}{2} \sqrt{64} = \frac{1}{2} \times 8 = 4$

Значит m = 4 см.

Ответ: 4 см.