Question

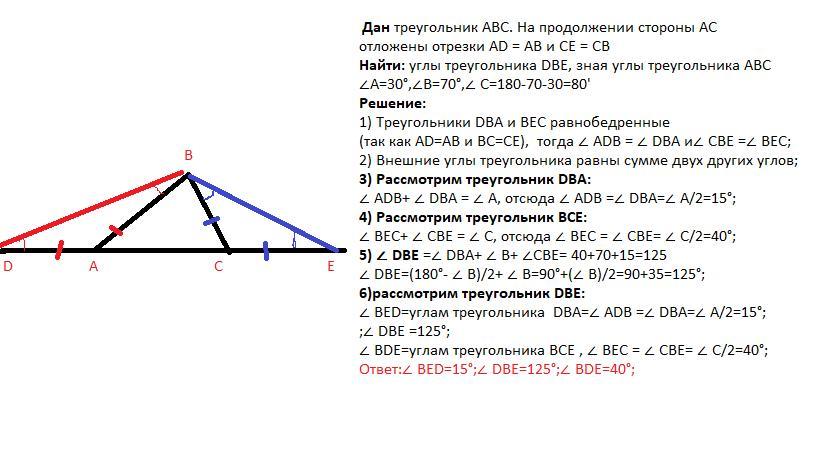
Дан треугольник АВС. На продолжении стороны АС за точку А отложен отрезок AD = АВ, а за точку С - отрезок СЕ = СВ. Найдите углы треугольника DBE, зная, что углы треугольника ABC кут A=30, кут B=70.

Answer 1

Відповідь:

Дано:

треугольник АBС.                                                                                                        На продолжении стороны АС отложены отрезки AD = АВ и СЕ = СВ

Найти:

углы треугольника DBE, зная углы треугольника АBС                                  ∠А=30°,∠В=70°,∠ С=180-70-30=80'

Решение:

1) Треугольники DBA и BEC равнобедренные (так как AD=AB и

BC=CE), тогда ∠ ADB = ∠ DBA и∠ CBE =∠ BEC;

2) Внешние углы треугольника равны сумме двух других углов;

3) Рассмотрим треугольник DBA:

∠ ADB+ ∠ DBA = ∠ A, отсюда ∠ ADB =∠ DBA=∠ A/2=15°;

4) Рассмотрим треугольник BCE:

∠ BEC+ ∠ CBE = ∠ C, отсюда ∠ BEC = ∠ CBE= ∠ C/2=40°;

5) ∠ DBE =∠ DBA+ ∠ B+ ∠CBE= 40+70+15=125

∠ DBE=(180°- ∠ B)/2+ ∠ B=90°+(∠ B)/2=90+35=125°;

6)рассмотрим треугольник DBЕ:

∠ BED=углам треугольника  DBA=∠ ADB =∠ DBA=∠ A/2=15°;

;∠ DBE =125°;

∠ BDE=углам треугольника ВСЕ , ∠ BEC = ∠ CBE= ∠ C/2=40°;

Ответ:∠ BED=15°;∠ DBE=125°;∠ BDE=40°;

Пояснення: