Question

Погибаю SOS! Помогите по геометрии

Answer 1

Ответ:

Радиус окружности, вписанной в правильный шестиугольник равен

$\bf a \frac{ \sqrt{3} }{2}$

Объяснение:

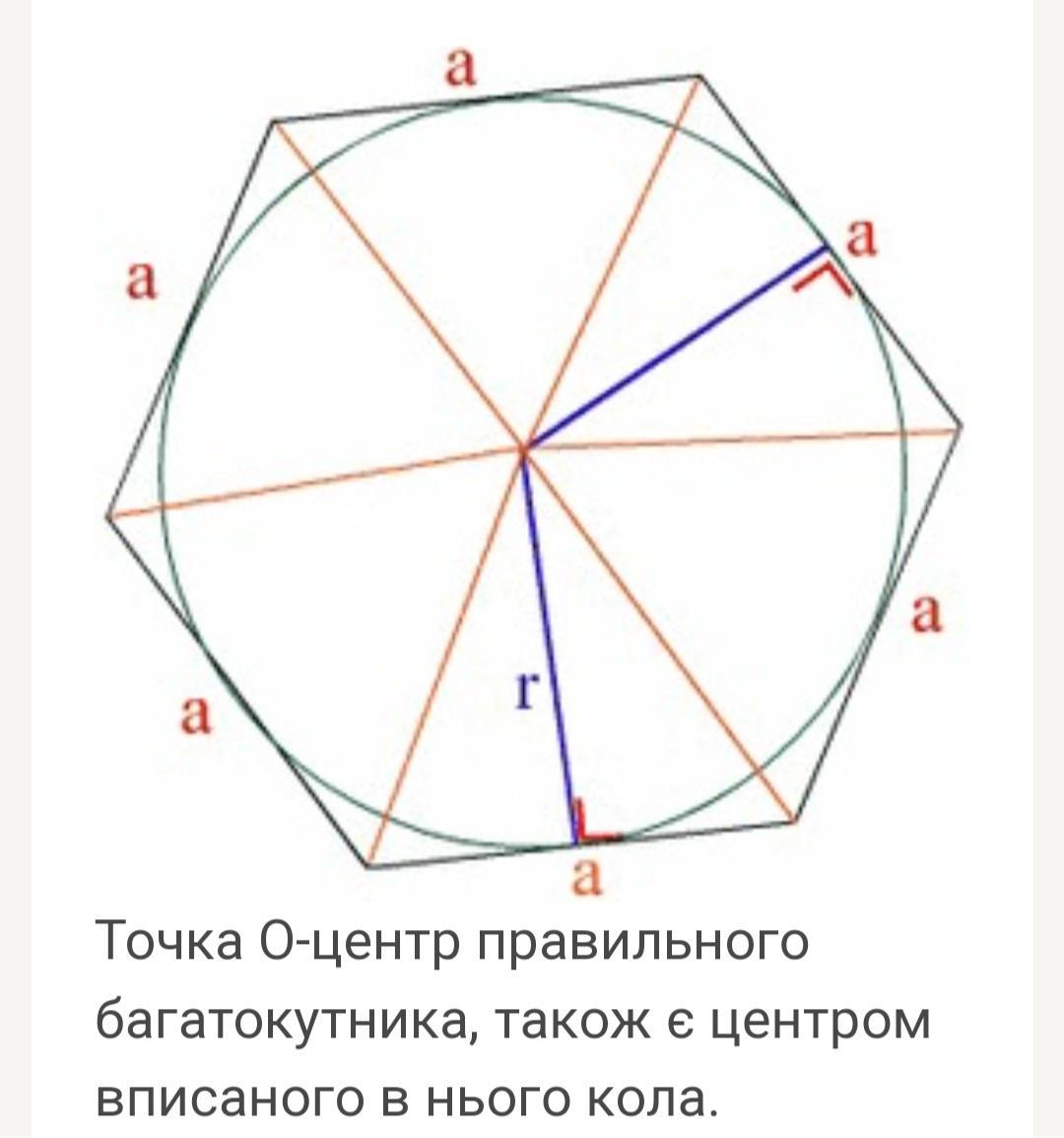
В правильной шестиугольник со стороной а вписана окружность. Найдите её радиус.

Что нам известно про правильный шестиугольник?

• Правильный шестиугольник - это шестиугольник, у которого все стороны равны между собой.
• Каждый угол правильного шестиугольника равен 120°
• Сторона правильного шестиугольника равна радиусу описанной окружности: а = R.

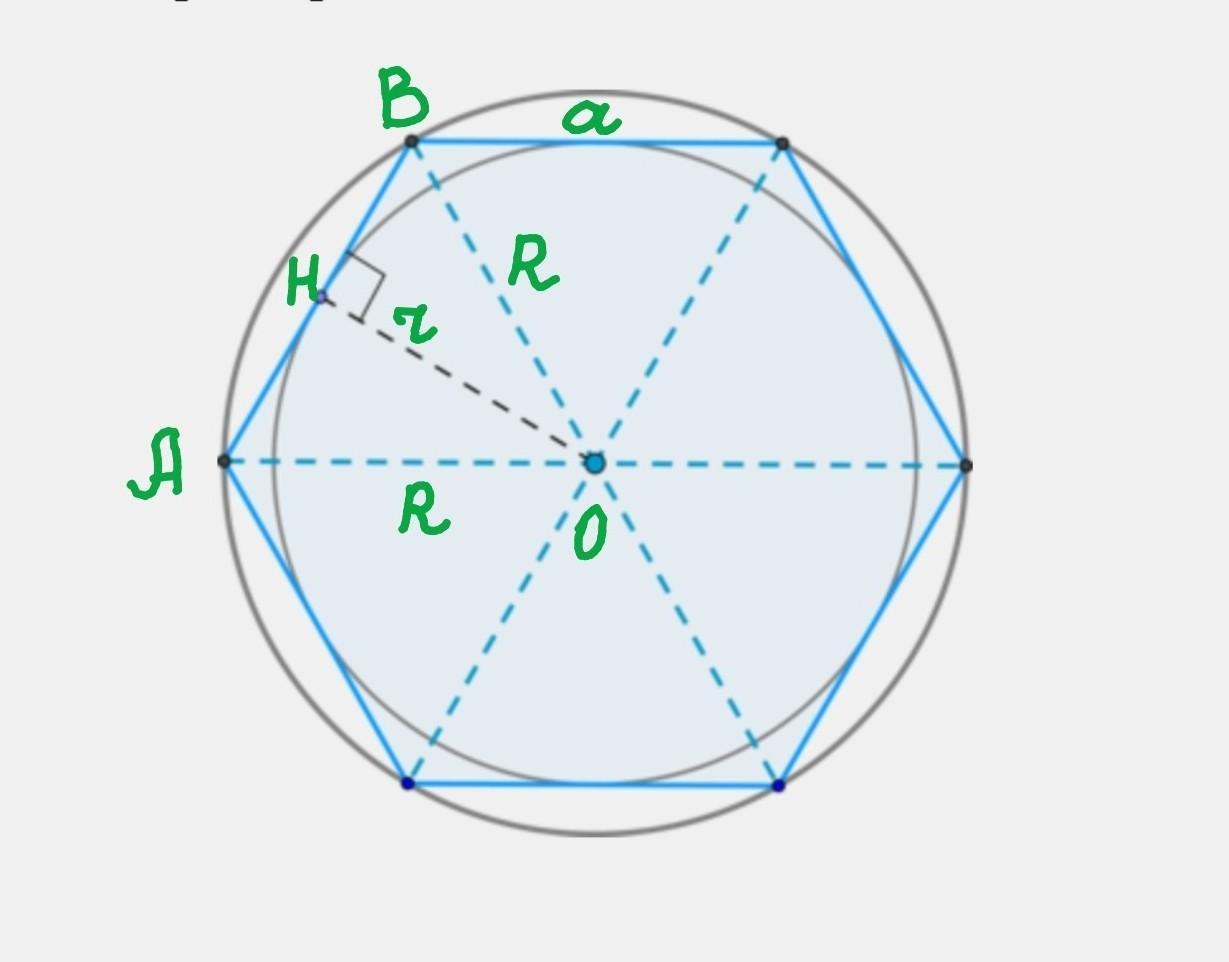
Радиус вписанной окружности нетрудно найти, рассмотрев равносторонний треугольник АОВ.

По свойству правильного шестиугольника радиус r вписанной окружности равен перпендикуляру ОН, проведённому из центра О (вписанной и описанной окружности) к стороне АВ = а.

Высота ОН в равнобедренном треугольнике (АО=ВО=R) является также медианой, поэтому

АН = ВН = ½ • АВ = ½ • а.

В прямоугольном треугольнике АНО(∠Н=90°): гипотенуза АО=R=a, катет АН=½•а.

По теореме Пифагора найдём катет ОН:

$OH = \sqrt{ {AO}^{2} - {AH}^{2} } = \sqrt{ {a}^{2} - \bigg(\dfrac{a}{2} \bigg)^2 } =$

$= \sqrt{ {a}^{2} - \dfrac{ {a}^{2} }{4} } = \sqrt{ \dfrac{3 {a}^{2} }{4} } = \bf \dfrac{a}{2} \sqrt{3}$

Таким образом, радиус вписанной окружности в правильном шестиугольнике равен:

$\boxed {\bf r = a \frac{ \sqrt{3} }{2} }$

#SPJ1

Answer 2

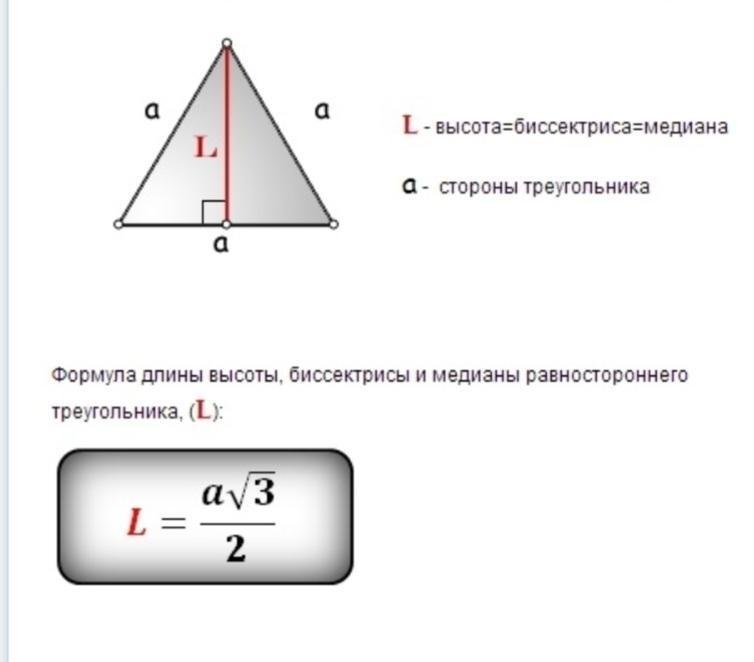
Відповідь: а√3/2

Пояснення:

відомий факт - діагоналі правильного шестикутника ділять шестикутник на 6 рівних правильних трикутників, де висота трикутника і є радіусом вписаного в шестикутник коло. Отже, r=а√3/2.

Див.скрін.