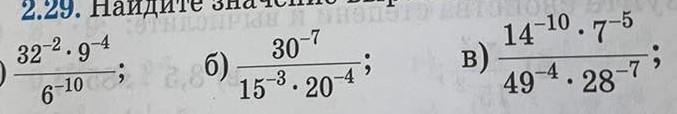Question

Помогите, с решением пожалуйста. ​

Answer 1

Ответ:

Пошаговое объяснение:

a)  32^(-2)*(9^(-4)/6^(-10) =6^10/(32^2*9^4) =>   разложим основания на простые множители:

6=2*3;   32 = 2^5;    9=3^2. Подставим в выражение:

(2^10*3^10) /(2^10*3^8) = 3^(10-8)=3^2 = 9.

**********

б)  30^(-7)/(15^(-3)*20^(-4)) = (15^3*20^4)/30^7=(15^3*10^4*2^4)/(15^7*2^7) =

= (15^(-4)*10^4*2^(-3)) = 10^4/(15^4*2^3) =  10000/(50625*8) =2/81.

*************

в)  (14^(-10)*7^(-5))/(49^(-4)*28^(-7))  =  (14^(-10)*7^(-5))/(7^(-8)*14^(-7)*2^(-7)) =

= 14^(-10-(-7))*7^(-5-(-8))/2^(-7)=(2^(-3)*7^(-3)*7^3)/2^(-7)=2^(-3-(-7)=2^4=16.

разложим основания на простые множители:

15 = 3*5;   20=2^2*5;  30 = 2*3*5.   Подставим в выражение:

(3^3*5^3*2^8*5^4)/(2^7*3^7*5^7) = 3^(3-7)*5^(3-7)*2^(8-7)*5^(4-7) =

= 3^(-4)*5^(-4)*2*5^(-3) =