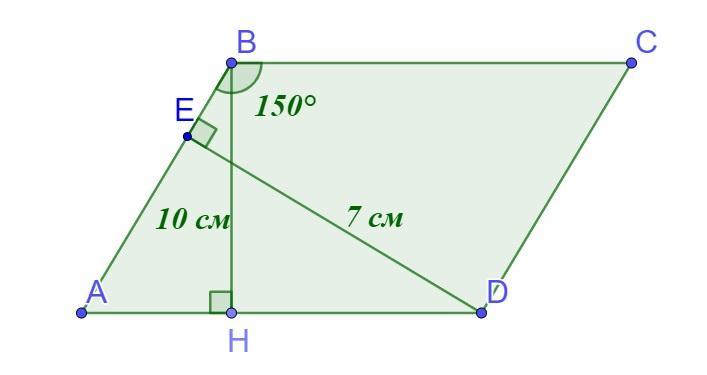
У паралелограмі ABCD проведено висоти ВН 1 DE. Знайдіть периметр паралелограма, якщо BH = 10 см, DE = 7CM <ABC = 150°
Помогите до 20:00
Распешите пожалуйста
Ответы
Ответ:
Периметр паралелограма дорівнює 68 см
Объяснение:
У паралелограмі ABCD проведено висоти ВН і DE. Знайдіть периметр паралелограма, якщо BH = 10 см, DE = 7 см, ∠ABC = 150°
За властивістю паралелограма: протилежні сторони у нього рівні.
Тому периметр паралелограма обчислюється за формулою:
Р = 2(a+b),
де а і b - сусідні сторони паралелограму.
Розв'язання:
Нехай маємо паралелограм ABCD, AB||CD і AD||BC, BН⊥AD, DE⊥АВ, де BН і DE– висоти паралелограма, опущені на сторони AD і АВ, відповідно. BH = 10 см, DE = 7 см.
∠ABC = 150° (за умовою), тоді:
∠А = 180° - ∠ABC = 180° - 150° = 30° - так як сума кутів, прилеглих до однієї сторони паралелограма, дорівнює 180° (за властивістю).
Розглянемо прямокутний ΔАВН (∠AНB=90°)
Катет ВН лежить навпроти кута А=30°, тому він дорівнює половині гіпотенузи АВ.
ВН = 1/2 · АВ.
Отже, АВ = 2 · ВН = 2 · 10 = 20 (см)
Розглянемо прямокутний ΔАED (∠AED=90°)
Катет DE лежить навпроти кута А=30°, тому він дорівнює половині гіпотенузи АD.
DE = 1/2 · АD.
Отже, АD = 2 · DE = 2 · 7 = 14 (см)
Периметр ABCD :
Р = 2 · (20+14) = 2 · 34 = 68 (см)
#SPJ1