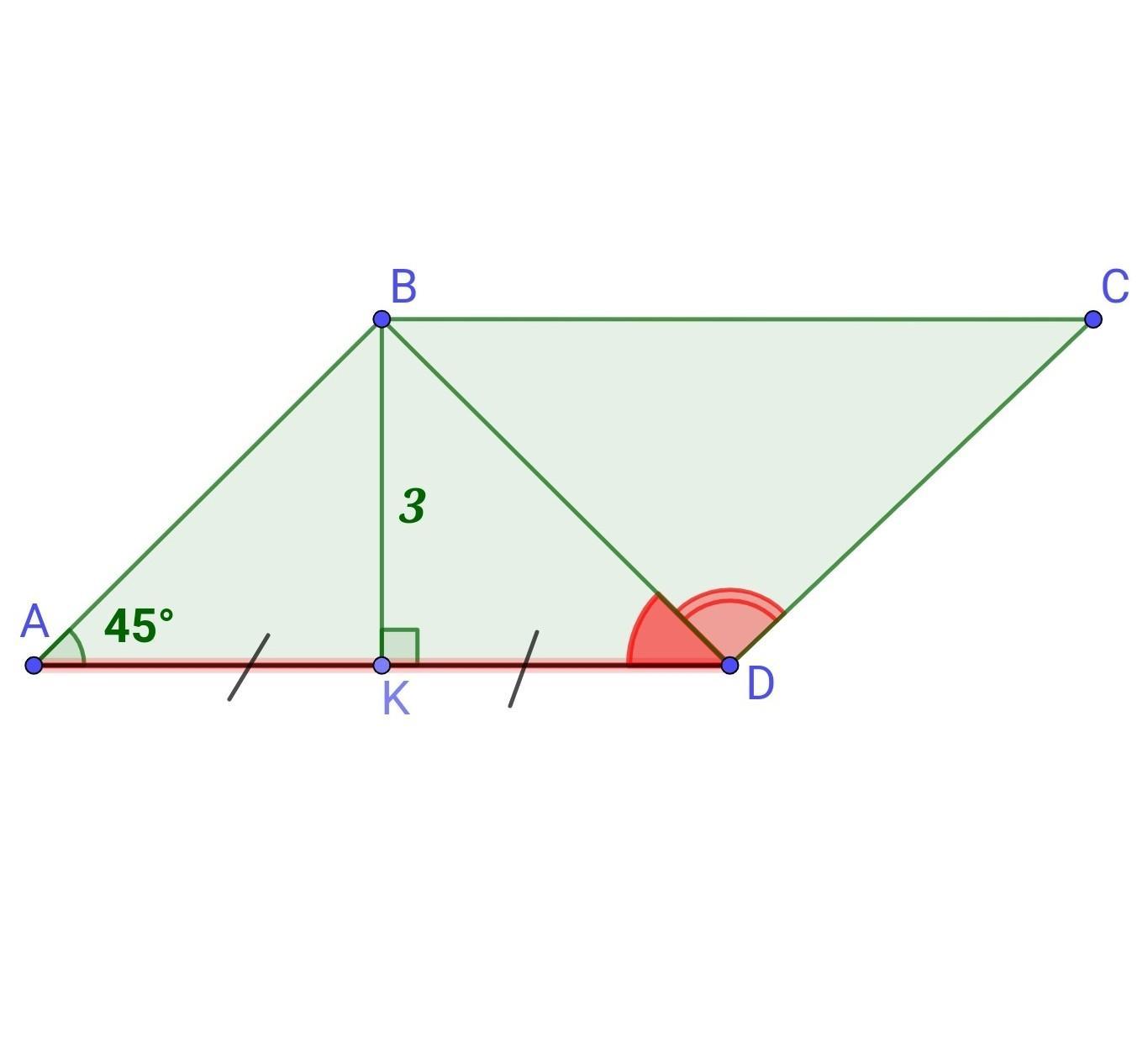
Один із кутів паралелограма дорівнює 45°. Його висота, проведена з вершини тупого кута, дорівнює 3 см і ділить сторону паралелограма навпіл. Знайдіть цю сторону паралелограма та кути які утворює діагональ що сполучає вершини тупих кутів зі сторонами паралелограма
Ответы
Ответ:
AD = 6 см; ∠ADB = 45°; ∠BDC = 90°.
Объяснение:
Один із кутів паралелограма дорівнює 45°. Його висота, проведена з вершини тупого кута, дорівнює 3 см і ділить сторону паралелограма навпіл. Знайдіть цю сторону паралелограма та кути які утворює діагональ що сполучає вершини тупих кутів зі сторонами паралелограма.
Нехай ABCD - даний паралелограм, ∠А = 45°, ВК⟂AD, ВК=3 см, AK=KD. BD - діагональ.
Знайдемо AD, ∠ADB, ∠BDC.
Розглянемо прямокутний трикутник ABK (∠K=90°).
За теоремою про суму гострих кутів прямокутного трикутника маємо:
∠А + ABK = 90°
Тоді ∠ABK=180°-∠A=90°-45°=45°.
Отже △АВК - рівнобедрений (за ознакою ) з основою АВ.
AK=BK=3 см - як бічні сторони рівнобедреного трикутника.
AD=2•AK, AD=2•3=6(см)
Розглянемо △ABD.
Висота BK є також медіаною △ABD, тоді △ABD - рівнобедрений з основою AD.
∠ADB=∠A=45° - як кути при основі рівнобедреного трикутника.
Висота в рівнобедреному трикутнику є також його бісектрисою, тоді:
∠ABD=2•∠ABK=2•45°=90°.
∠BDC=∠ABD=90° - як внутрішні різносторонні кути при перетині паралельних прямих AB і DC січною BD.
#SPJ1