Ответы
Ответ дал:
3
Ответ:
∠A = ∠C = 45°, ∠B = ∠D = 135°.
Объяснение:
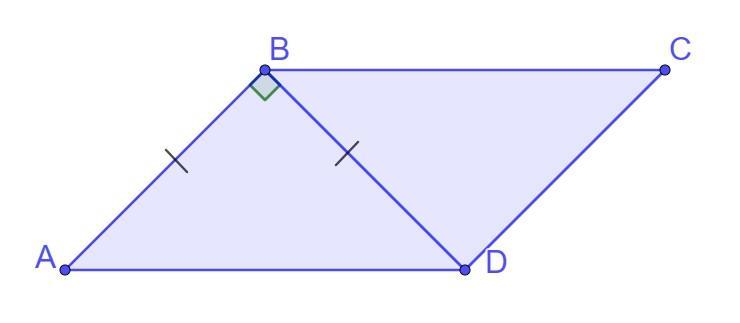
Знайдіть кути паралелограма ABCD, якщо BD⊥AB i BD=AB.
Дано: ABCD - паралелограм, BD - діагональ, BD⊥AB, BD=AB.
Знайти: ∠A, ∠B, ∠C, ∠D.
Розв'язання
1) Розглянемо ΔABD (∠ABD = 90°).
BD=AB, отже ΔABD - рівнобедрений з основою AD.
Кути при основі рівнобедреного трикутника рівні, тому:
∠BAD = ∠BDA = (180° - ∠ABD) : 2 = (180°-90°) : 2 = 45°.
Отже ∠A = ∠C = 45° - за властивістю протилежних кутів паралелограма.
2) За властивістю сусідніх кутів паралелограма маємо:
∠А + ∠В = 180°
Тоді:
∠В = 180° - ∠А = 180° - 45° = 135°
∠B = ∠D = 135° - за властивістю протилежних кутів паралелограма.
Відповідь: ∠A = ∠C = 45°, ∠B = ∠D = 135°.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад