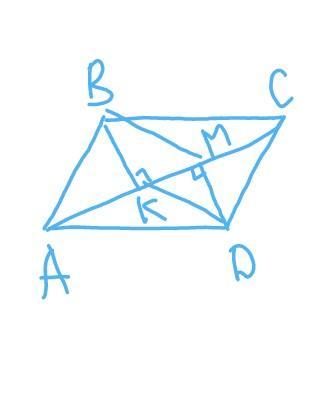
В параллелограмме ABCD из вершин B и D опустили
перпендикуляры BK и DM на диагональ AC. Докажите, что
BMDK – параллелограмм.
Ответы
Ответ дал:
4
Объяснение:
Диагональ АС делит параллелограмм на 2 равных треугольника АВС и СDA , значит
ВК=DM.
∆BKM=∆DMK - по 2 катетам (ВК=DM ;
KM - общая), следовательно, ВМ = DM.
Eсли в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник- параллелограмм.
что и требовалось доказать.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад