I
M
с
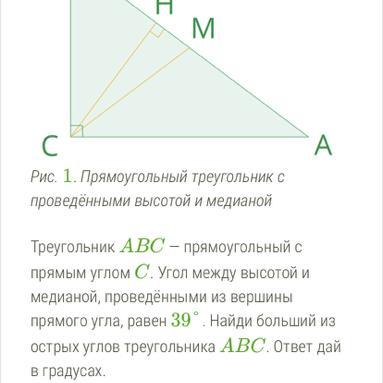
Рис. 1. Прямоугольный треугольник с
проведёнными высотой и медианой
A
Треугольник АВС - прямоугольный с
прямым углом С. Угол между высотой и
медианой, проведёнными из вершины
прямого угла, равен 39°. Найди больший из
острых углов треугольника ABC. Ответ дай
в градусах.
Приложения:
Ответы
Ответ дал:
0
ля решения задачи воспользуемся свойствами прямоугольного треугольника.
Пусть угол BAC - больший острый угол треугольника ABC.
Так как треугольник ABC прямоугольный, то угол BAC + угол ABC + угол BCA = 180 градусов.
Угол ABC = 90 градусов (прямой угол).
Тогда угол BCA = 180 - угол BAC - угол ABC = 180 - угол BAC - 90 = 90 - угол BAC.
Угол между высотой и медианой, проведёнными из вершины прямого угла, равен 39 градусам.
Так как высота и медиана являются перпендикулярами, то угол BCA равен 39 градусам.
Тогда 90 - угол BAC = 39 градусов.
Угол BAC = 90 - 39 = 51 градус.
Таким образом, больший из острых углов треугольника ABC равен 51 градус.
Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад
8 лет назад