Ответы
Ответ дал:
3
Ответ:
Применяем формулы квадрата суммы и квадрата разности :
.
Исходя из этих формул выделяем полные квадраты :
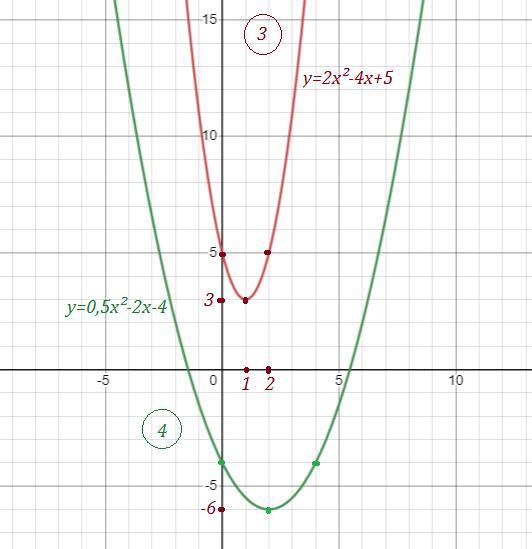
Вершина в точке ( 3 ; 3 ) .
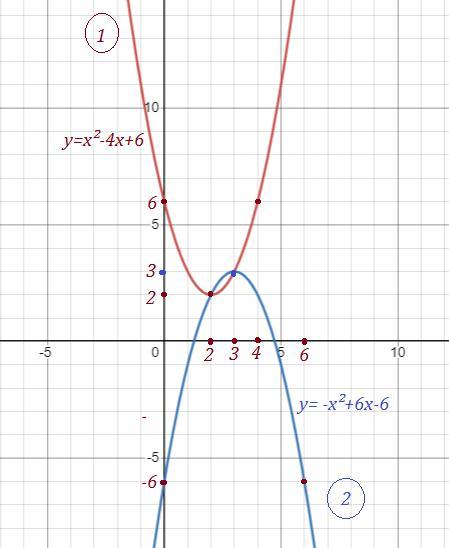
Вершина в точке ( 2 ; -6 ) .
Графики функций во вложении .
Приложения:


fctdgsygfdhngfxzgsac:
Alnadya, здравствуйте! можете помочь пожалуйста? у меня в профиле есть 6 задания с границами последовательностей, прошу помогите
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
