Question

Помогите пожалуйста!!!
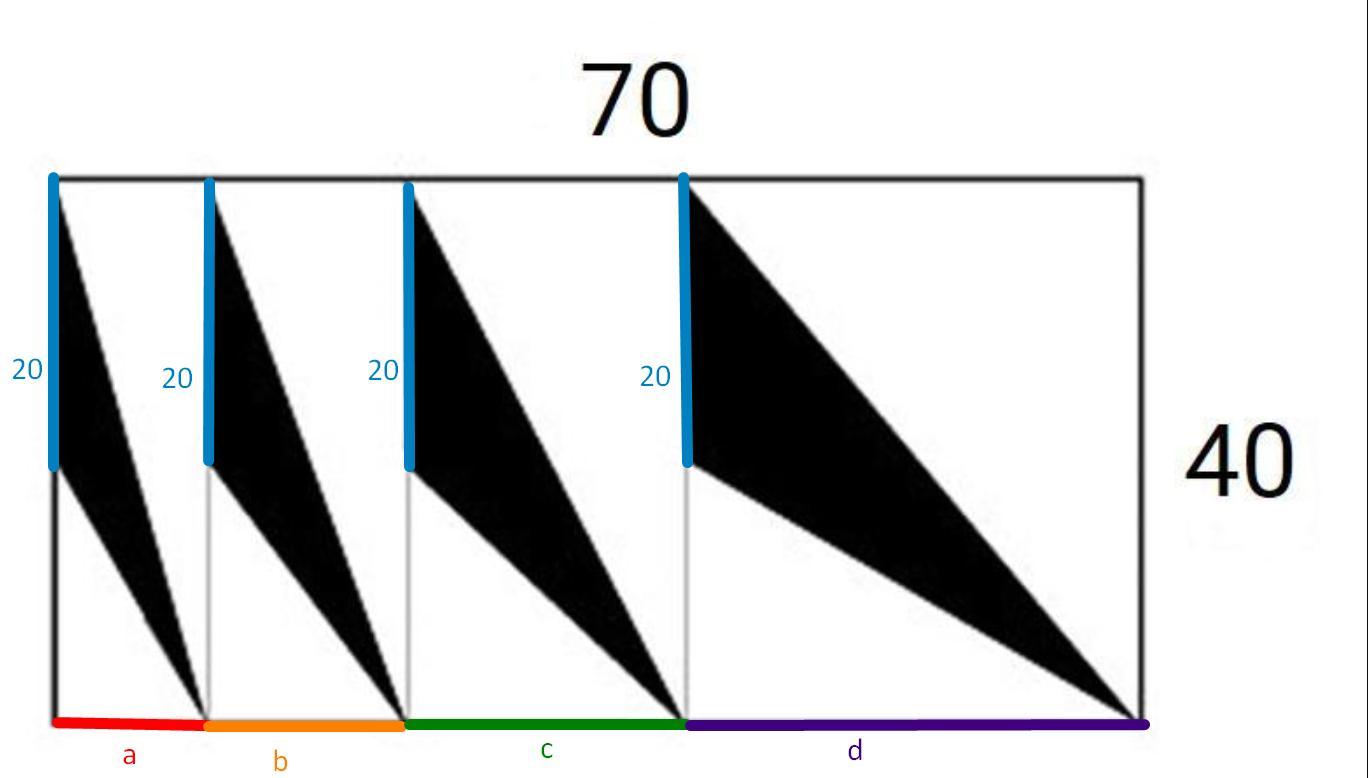
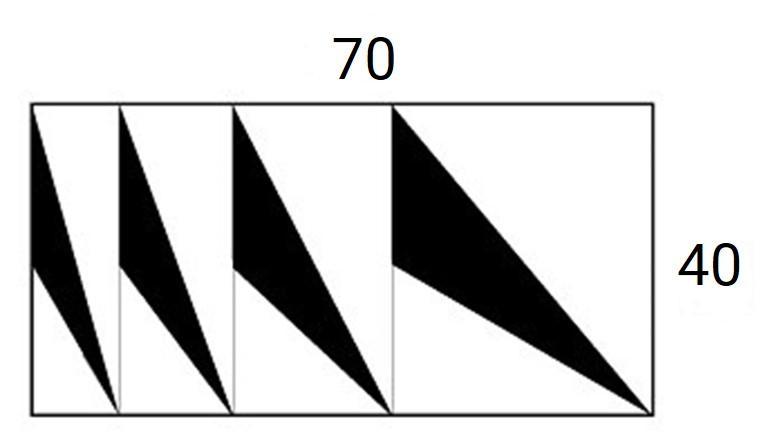
Для своего арт-проекта Иван разделил белый холст размером 40×70
см на прямоугольные области, как показано на рисунке, и нарисовал в каждой области чёрный треугольник.
Крайняя левая сторона каждого чёрного треугольника составляет ровно 20
см. Найдите площадь части холста, оставшейся белой. Ответ выразите в квадратных сантиметрах.

Answer 1

Ответ: Площадь части холста, оставшейся белой равна 2100 см²

Пошаговое объяснение:

Пусть  высота первого черного треугольника равна a, второго b, третьего c, и у четвертого d, по условию основание каждого из них равно 20 см (т.е крайняя левая сторона)

Теперь вспомним, что площадь треугольника можно вычислить по формуле

$S_{\triangle} = \dfrac{1}{2} ah$

Обозначим площадь каждого из этих треугольников как

S₁, S₂, S₃, S₄

И сразу посчитаем их сумму
$\displaystyle S_ 1 + S_ 2 + S_3 + S_4 = \dfrac{1}{2}\cdot 20 \cdot a + \dfrac{1}{2}\cdot 20 \cdot b + \dfrac{1}{2}\cdot 20 \cdot c + \dfrac{1}{2}\cdot 20 \cdot d = \\\\\ = \frac{20}{2}(a + b + c + d) = 10 (a+ b + c + d)$

Теперь важно понять, что a + b + c + d = 70, поскольку они являются частями стороны которая противоположна и равна 70

Следовательно площадь черной части холста

S₁ +  S₂ +  S₃ +  S₄ = 10·(a + b + c + d) = 10·70 = 700 см²

Площадь всего холста равна 70·40 = 2800 см²

Соответственно площадь части холста, оставшийся белой равна

2800 - 700 = 2100 см²

#SPJ1