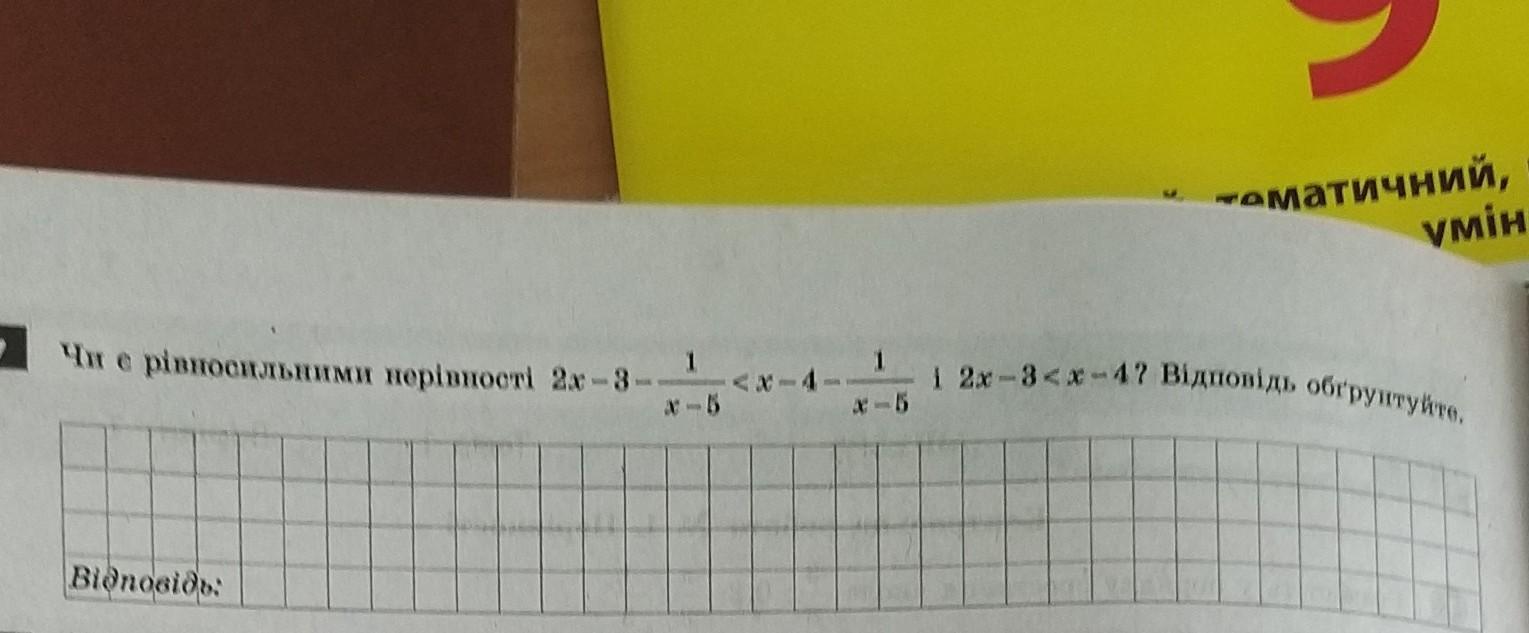Question

чи є рівносильними нерівності 2х-3-1/х-5<х-4-1/х-5 і 2х-3<х-4?​

Answer 1

Ответ:

МОЖНА КОАЩУ ВІДПОВІДЬ=3

Объяснение:

Для визначення, чи є нерівності 2x - 3 - 1/(x - 5) < x - 4 - 1/(x - 5) та 2x - 3 < x - 4 рівносильними, спростимо першу нерівність.

Спочатку відсутні знаменники в обох частині нерівності, оскільки вирази 1/(x - 5) відсутні в обох частинах:

2x - 3 - 1/(x - 5) < x - 4 - 1/(x - 5)

Тепер відняємо (x - 5) від обох сторін:

2x - 3 - 1 < x - 4 - 1

Зараз вирази 1 відсутні в обох частинах, і ми отримуємо:

2x - 3 < x - 4

Тепер віднімемо x від обох сторін:

x - 3 < -4

Потім додамо 3 до обох сторін:

x < -1

Тепер ми маємо нерівність 2x - 3 < x - 4, яка рівносильна x < -1. Тобто, обидві нерівності рівносильні, і вони вказують на те, що x має бути менше -1.