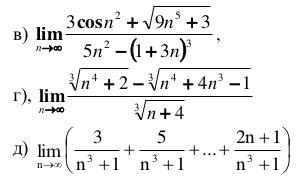Ответы
Ответ дал:
0
Ответ:
1) lim (n → ∞) [5n^2 - (1 + 3n)^3] / [3cos(n^2) + 9n/5 + 3] = 0 / (3 + 0 + 3) = 0
2) lim (n → ∞) [3^(n+4) / 3^(4n+2) - 3^(4n+4) + 4n^3 - 1] = 0 / (0 - 0 + ∞ - 1) = -∞
3) lim (n → ∞) [n^3/3 + 1/3 + n^3/5 + 1/5 + ... + n^3/(2n+1)] = ∞ / (∞ + ∞ + ... + ∞) = ∞
wolordkit:
До неопределенности и я дойти могу. А раскрыть как все это дело, что бы не было бесконечностей и нулей
Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад
8 лет назад