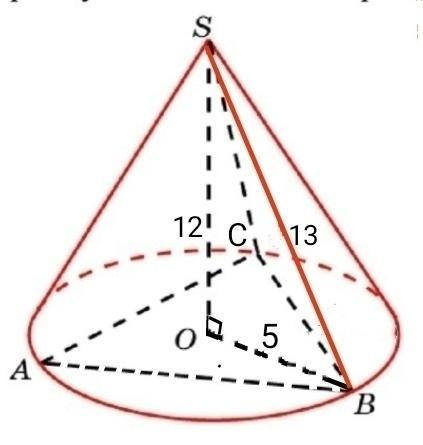
У конус із твірною 13см і висотою 12см вписано правильну трикутну піраміду.
Знайдіть площу основи цієї піраміди.
zmeura1204:
Т.Піфагора: R=√(13²-12²)=5; a=R√3=5√3; S=a²√3/4=(5√3)²√3/4=18,75√3
Повна відповідь будь ласка
Це повна відповідь.
На зображенні з поясненням, будь ласка, мені потрібно здати сьогодні
Ответы
Ответ дал:
2
Ответ:
75√3/4 см².
Объяснение:
Если в конус вписана правильная пирамида, то вершины конуса и пирамиды совпадают, и правильный треугольник, являющийся основанием данной пирамиды. вписан в круг, лежащий в основании конуса.
1. Высота конуса h, его образующая l и радиус основания R образуют прямоугольный треугольник.
По теореме Пифагора
l² = h² + R².
По условию
R² = 13² - 12² = 25, тогда R = 5 см.
2. Правильный треугольник вписан в круг, тогда по теореме его сторона а3 может быть найдена по формуле:
а3 = R√3.
В нашем случае
а3 = 5√3 см.
3. Основанием данной пирамиды является равносторонний треугольник.
Площадь правильного треугольника находим по формуле:
S = a²√3/4
S = (5√3)²•√3/4 = 25 • 3 • √3/4 = 75√3/4 (см²).
Приложения:
Всё ли понятно?
Краще було на українському мові
А Вы допускаете то, что я не владею украинским языком в той степени, чтобы писать решение здесь именно на украинском? Я помогла с решением, идеей. Оформить решение на Вашем языке обязательно помогут другие пользователи. Доброго дня и удачи на "Знаниях")
Ладно, но тоже спасибо
пишите на русском, eбаный в рот, вы типа не понимаете что здесь написано? что кругом один хохляндский язык
в кои то веки поддержу магистра
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад
8 лет назад