Ответы
Ответ дал:
0
Ответ: 1/2 кв.ед.
Объяснение:
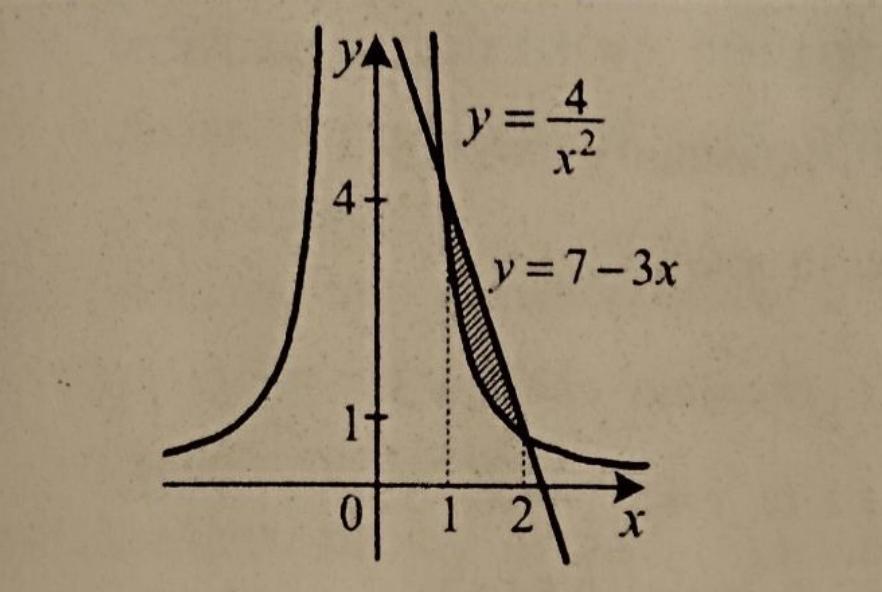
Площадь S=∫(a;b)f1(x)dx - ∫(a;b)f2(x)dx.
Ghgtltks интегрирования a=1; b=2/
f1(x) = 7-3x;
f2(x) = 4/x^2. Тогда
S=∫(1;2)(7-3x)dx - ∫(1;2)(4/x^2)dx = 5/2-2 = 1/2 кв.ед.
1) ∫(1;2)(7-3x)dx = ∫(1;2)7dx - ∫(1;2)3xdx = 7(x)|(1;2)-3/2 (x^2)|(1;2) =
= 7(2-1) - 3/2(2^2-1^2) = 7*1 - 3/2(4-1) = 7-9/2 = 7-4 1/2 = 2 1/2 = 5/2 кв.ед.
2) ∫(1;2)(4/x^2)dx = -4/x|(1;2) = -4(1/2-1/1) = -4*(-1/2) = 2 кв.ед.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад