Спростити вираз
((2+sqrt(3))/(sqrt(2)+sqrt(2+sqrt(3)))+(2-sqrt(3))/(sqrt(2)-sqrt(2-sqrt(3))))
Приложения:
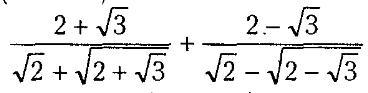
Ответы
Ответ дал:
1
Ответ:
Нам потребуется выделение полного квадрата из подкоренного выражения . Я заранее напишу эти действия , чтобы потом было понятно, что откуда берётся .
Аналогично
Теперь упростим выражение .
Приложения:


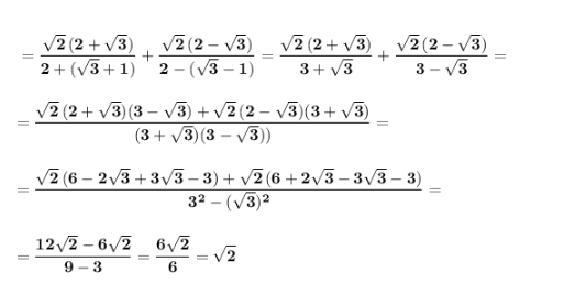
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад