Основою піраміди є рівнобічна трапеція, бічна сторона якої дорівнює 4 см, а діагоналі ділять гострі кути трапеції навпіл. Знайдіть висоту піраміди, якщо гострий кут трапеції дорівнює 60°, а всі бічні ребра піраміди утворюють з площиною основи кут 30°.
Ответы
Ответ дал:
2
Если боковые ребра пирамиды образуют с плоскостью основания равные углы, то вершина падет в центр описанной окружности основания.
∠ADB=60/2=30 (DB -биссектриса)
AB/sin30 =2R => R=AB=4
SO =R tg30 =4/√3
Приложения:
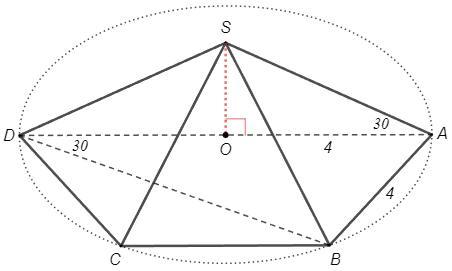
Треугольник ABD с углами 30, 60 - прямоугольный, центр описанной окружности - середина гипотенузы. Но нам достаточно, что в любом треугольнике с углом 30 сторона против этого угла равны радиусу описанной окружности.
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад
А почему центр описанной окружности на отрезке АД?