Ответы
Ответ:
20π см.
Объяснение:
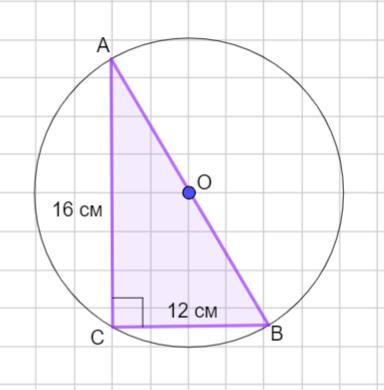
Найти длину окружности, описанной около прямоугольного треугольника с катетами 12 и 16 см.
Пусть дан Δ АВС - прямоугольный ( ∠С =90°) АС = 16 см, ВС =12 см.
Длина окружности определяется по формуле:
С =2πR, где R - радиус окружности.
Так как центр окружности, описанной около прямоугольного треугольника находится в середине гипотенузы, то радиус этой окружности равен половине гипотенузы.
Найдем гипотенузу АВ прямоугольного треугольника. Для этого воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АВ² = АС ² +ВС²;
АВ² = 16² +12² = 256 + 144 = 400
АВ = √400 = 20 см.
Тогда радиус окружности, описанной около этого треугольника
R= АВ : 2;
R= 20 : 2 = 10 см.
Найдем длину окружности
С = 2 ·π· 10 = 20π см.
#SPJ1