Question

На стороне BC прямоугольника ABCD взята точка E.Докажите,что площадь прямоугольника равна удвоенной площади треугольника AED.

Answer 1

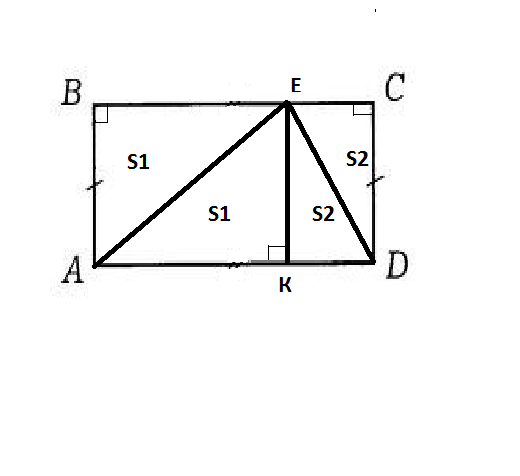
1) дополнительное построение: АЕ, ЕК⊥AD, ЕD ( см. рис), тогда 

  ΔАВЕ = ΔВЕК, Δ ВСD = ΔВКD.

! Равные фигуры имеют равные площади, тогда

 S abcd = 2·(S1+S2),где S1- площадь   ΔАВЕ, S2- площадь   Δ ВСD.

2)Из Δ AED: !!!площадь фигуры равна сумме площадей фигур из которых она состоит, значит Saed = S1+S2 .

  Таким образом   S abcd =2· Saed, что и тр. доказать.