Question

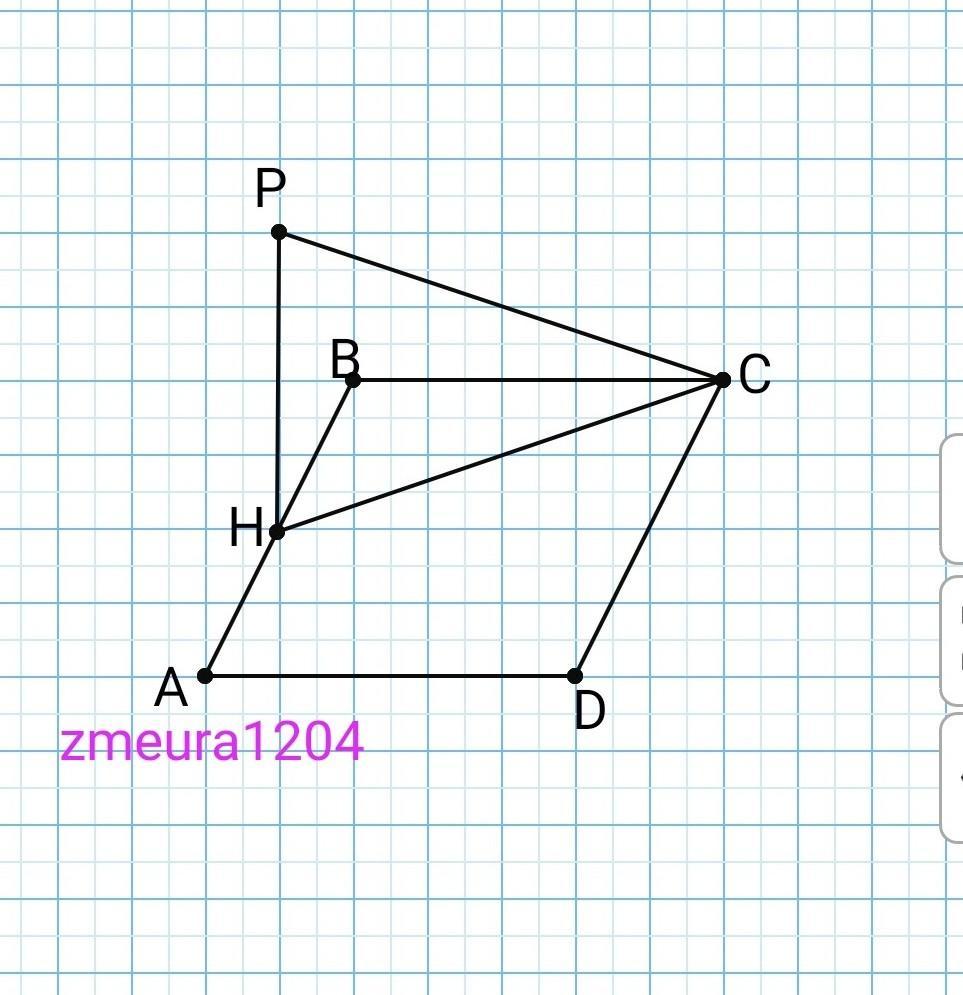
СРОЧНО ДАЮ 100 БАЛОВ! Через середину Н сторони АВ квадрата ABCD проведено до його площини перпендикуляр РН, довжина якого №5 см. Сторона квадрата дорівнюють 8/5 5 см. Виконайте побудову та обчисліть:

1)Відстань від точки Р до вершини квадрата С

2)Площу трикутника НВС
Обов'язково потрібне розв'язання.

Answer 1

Ответ:

Відстань від точки Р до вершини С дорівнює √21см

Площа трикутника ∆НВС дорівнює 32√10см²

Объяснение:

ВН=АВ/2=8√5/5:2=8√5/10см

ВС=8√5/5см

∆ВНС- прямокутний трикутник

Теорема Піфагора:

НС=√(ВН²+ВС²)=

=√((8√5/5)²+(8√5/10)²)=

=√(320/25+320/100)=

=√(320*4/25*4+320/100)=

=√((1280+320)/100)=√(1600/100)=

=4см.

∆РНС- прямокутний трикутник.

Теорема Піфагора:

РС=√(НС²+РН²)=√((√5)²+4²)=

=√(5+16)=√21см

__________

S(∆HBC)=½*HB*BC=

=½*8√5/10*8√5/5=32√10см²