Ответы
Ответ:
Доказано, что КМЕР - параллелограмм.
Пошаговое объяснение:
Доказать, что в каждом выпуклом
четырехугольнике середины сторон являются вершинами некоторого параллелограмма.
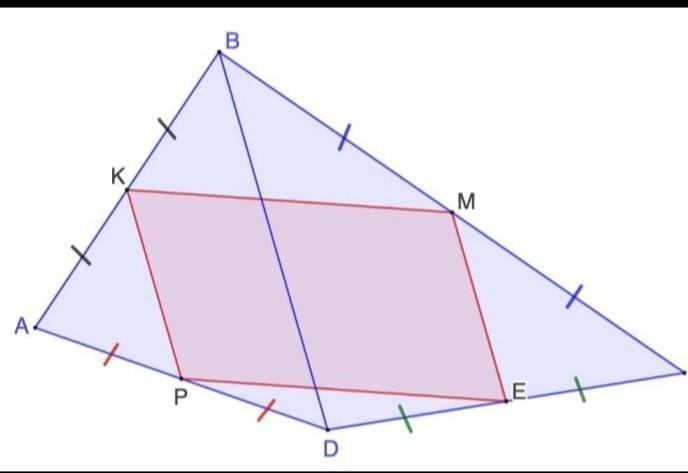
Дано: ABCD - выпуклый четырехугольник; AK = KB; BM = MC; CE = ED; DP = PA.
Доказать: КМЕР - параллелограмм.
Доказательство:
Проведем диагональ BD.
1. Рассмотрим ДАВО.
AK = KB; DP = РА (по условию)
→ РК - средняя линия.
• Средняя линия равна половине длины стороны, которую она не пересекает, и параллельна ей.
⇒ PK || BD; PK = 1/2 BD
2. Рассмотрим ДДВС.
BM = MC; CE = ED (по условию)
→ МЕ - средняя линия.
⇒ ME || BD; ME = 1/2 BD
3. Рассмотрим КМЕР.
PK = 1/2 BD
ME = 1/2 BD
→ PK = ME
PK II BD
ME || BD
Если две прямые параллельны третьей, то они параллельны между собой.
→ PK || ME
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
⇒ КМЕР - параллелограмм.
Этот параллелограмм называют параллелограммом Вариньона.