Question

Расстояние между центрами окружностей радиусов 2 и 1 равно $sqrt{3}$ . Найдите площади образовавшихся луночек и общей части кругов.

Answer 1

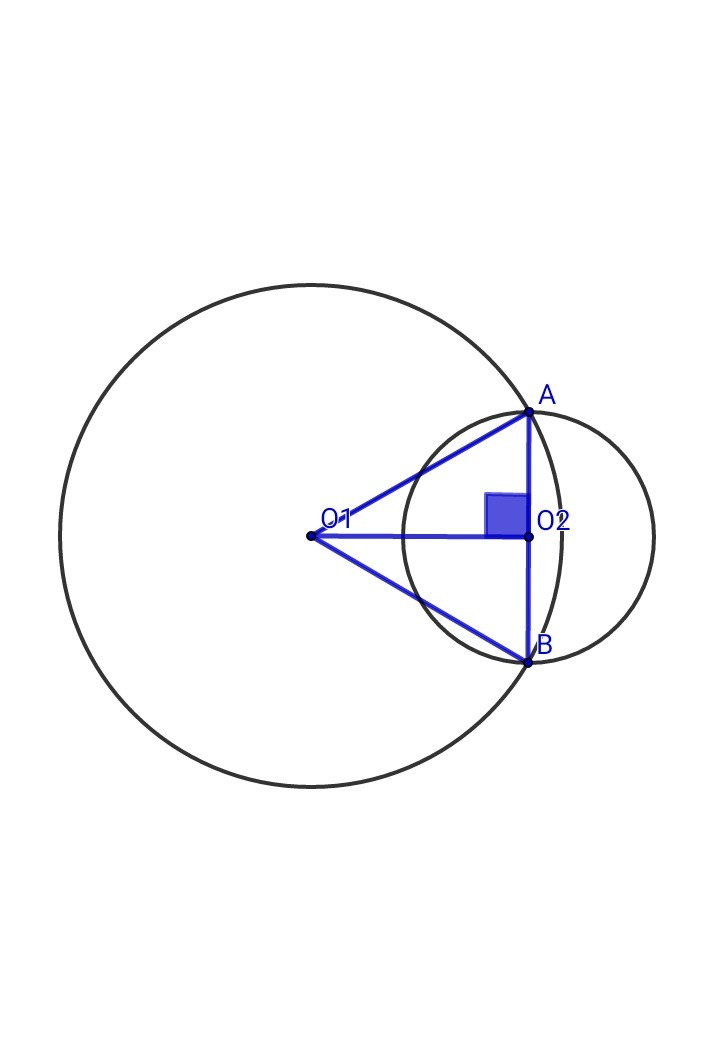
AO₁ = 2 , AO₂ = 1 , O₁O₂ = √3

Для ΔАО₁О₂ выполняется теорема Пифагора: АО₁² = О₁О₂² + АО₂² ;  2² = (√3)² + 1²  ;  4 = 4  ⇒  ΔАO₁O₂ - прямоугольный, O₁O₂⊥AB

ΔАО₁В - равнобедренный, АО₁ = BO₁ = 2 ⇒ O₁O₂⊥AB, AO₂ = BO₂ = 1

AO₁ = BO₁ = AB = 2  ⇒ ΔAO₁B - равносторонний

Площадь круга с радиусом R₁ = 2:  S₁ = πR₁² = 4π

Плoшадь круга с радиусом R₂ = 1:  S = π  

S ao₁b = AB²√3/4 = 4√3/4 = √3

Площадь ме'ньшего сектора, соединяющего точки А, О₁, В:

S сек. = πR₁²•α/360° = π•R₁²•∠AO₁B/360° = 4π•60°/360° = 2π/3

S ceк. = S ao₁b + S

S = S сек. - S ao₁b = (2π/3) - √3

Площадь общей части кругов:  S₃ = (S₂/2) + S = (π/2) + (2π/3) - √3 = (7π/6) - √3

Площадь бо'льшей луночки: S₄ = S₁ - S₃ = 4π - (  (7π/6) - √3  ) = 4π - (7π/6) + √3 = (17π/6) + √3

Площадь ме'ньшей луночки: S₅ = (S₂/2) - S = (π/2) - (  (2π/3) - √3  ) = (π/2) - (2π/3) + √3 = √3 - (π/6)