Question

В окружности проведены хорды AC и BD так, что они пересекаются в точке
P. Докажите, что угол APB равен полусумме угловых величин дуг
AB и CD.

Answer 1

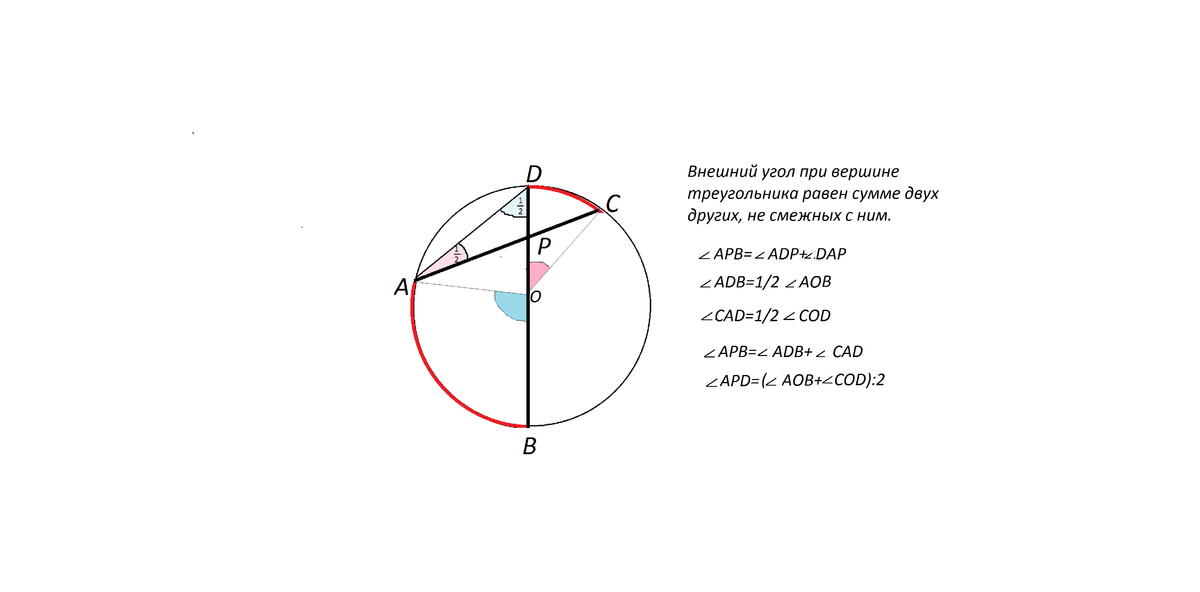
  Соединим точки А и Д. 
Углы ДАС и АДВ вписанные и каждый равен половине угловой величины дуги, на которую опирается.
Сумма этих углов равна половине суммы угловой величины дуг, на которые они опираются.
Угол АРВ - внешний угол при вершине Р треугольника АРД и равен сумме углов ДАС и АДВ. 
Следовательно, угол АРВ, равный сумме углов АДВ и ДАС, равен полусумме угловых величин дуг АВ и СД.