Question

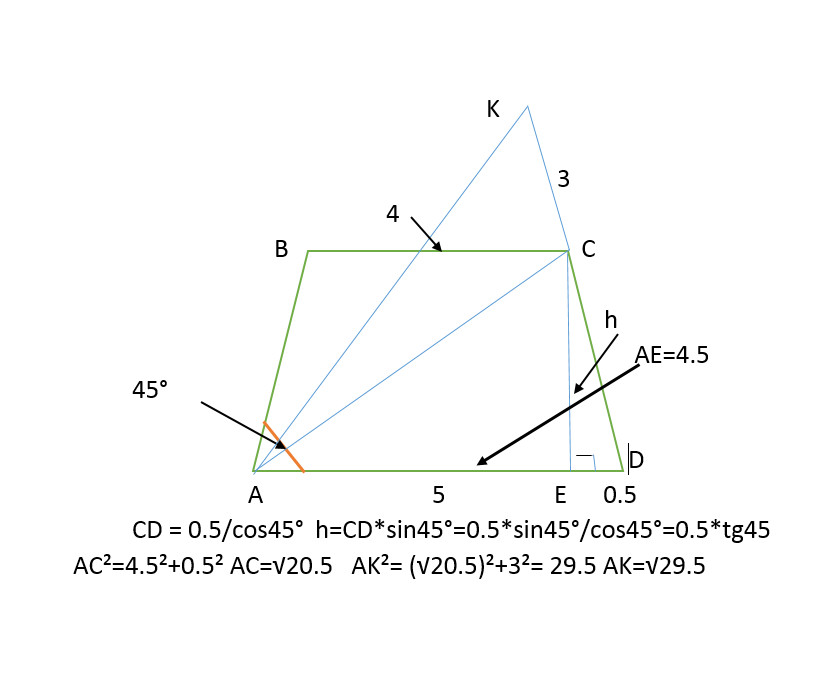
Дана равнобедренная трапеция ABCD с основанием 4 и 5 см.Угол BAD равен 45 градусов.Из вершнины трапеции С восстановлен перпендикуляр к плоскости трапеции СК длиной 3 см. Найти расстояние от вершины перпендикуляра К до точки А.

Answer 1

ED = 0.5
AE = AD - ED = 5 -0.5 =4.5
ED = CD*cos45°
CD = ED/cos45°
CD = 0.5/cos45°
h=CD*sin45°=0.5*sin45°/cos45°=0.5*tg45° 
tg45°=1
h = 0.5
AC²  = AE² + h² = 4.5²+0.5² = 20.5
AC =√20.5 
AK²= AC² + KC² = (√20.5)²+3²= 20.5 + 9 =29.5
AK² =29.5
AK=√29.5 расстояние от A до K
смотри рисунок точка К над трапецией в воздухе