Question

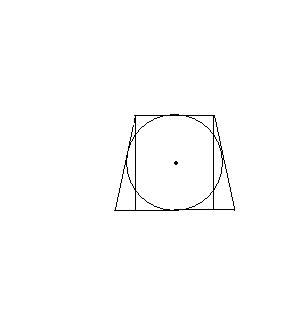
Найти площадь трапеции, описанной вокруг окружности, если разница основ равна 14 см, а боковые стороны - 13 см и 15 см.

Answer 1

Использовано свойство сторон 4-хугольника, описанного около окружности; теорема Пифагора; формула площади трапеции

Answer 2

Суммы противоположных сторон в такой трапеции равны. a+c=b+d

Верхнее основание b = [(a+c)-d]/2 = [(13+15)-14]/2 = 7см, нижнее - 7+14 = 21см

S = (b+d)*h/2

Высоту попытаемся найти из треугольников, опустив 2 высоты на нижнее основание:

h²=13²-x²

h²=15²-(14-x)²

15²-(14-x)²=13²-x²

225 - 196 + 28x - x² = 169 - x²

28x = 140

 x = 5

h = √13²-5² = √144 = 12cм

S = (13+15)*12/2 = 168см²