Question

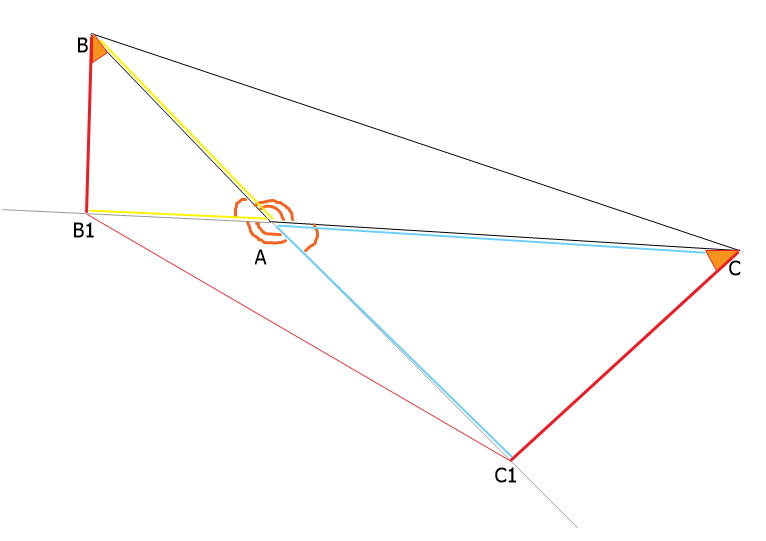
В треугольнике ABC  с тупым углом BAC  проведены высоты BB1  и CC1 . Докажите, что треугольники B1AC1  и ABC  подобны.

Answer 1

та как треугольники ВСС1 и ВСВ1 - прямоугольные, то их можно описать окружностью, диаметр которой совпадает с общей гипотенузой ВС
угол ВС1В1 и угол ВСВ1 - опираются на одну и ту же дугу окружности
значит угол ВС1В1 и угол ВСВ1 - равны а значит угол АС1В1 и угол ВСА - равны
угол С1В1С и угол С1ВС - опираются на одну и ту же дугу окружности
значит угол С1В1С и угол С1ВС - равны а значит угол С1В1А и угол АВС - равны
так как угол АС1В1 и угол ВСА - равны
так как угол С1В1А и угол АВС - равны
так как угол ВАС и угол В1АС1 - равны
то треугольники АВС и АВ1С1 - подобны  - доказано

Answer 2

подобие получившихся прямоугольных треугольников доказывается легко:
прямоугольные треугольники с двумя вертикальными ((равными))) углами --- 
подобны по двум углам...
т.е. углы В1ВА и С1СА равны)))
запишем соответствующую пропорцию:
ВВ1 / СС1 = АВ1 / АС1 = АВ / АС (((гипотенузы всегда пропорциональны...))) 
последнее равенство можно переписать так: 
((по свойству пропорции... произведение крайних членов = произведению средних членов))) АВ1*АС = АС1*АВ или так: 
АВ1 / АВ = АС1 / АС
Это равенство читается так: стороны треугольника АВ1С1 пропорциональны сторонам треугольника АВС (((две стороны))),
АВ1 пропорциональна АВ
АС1 пропорциональна АС... 
а т.к углы между этими сторонами равны (((как вертикальные))) --- то по второму признаку подобия треугольников ---
треугольники АВ1С1 и АВС подобны)))))
Второй признак подобия:
Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы, 
заключенные между этими сторонами, равны, 
то такие треугольники подобны)))