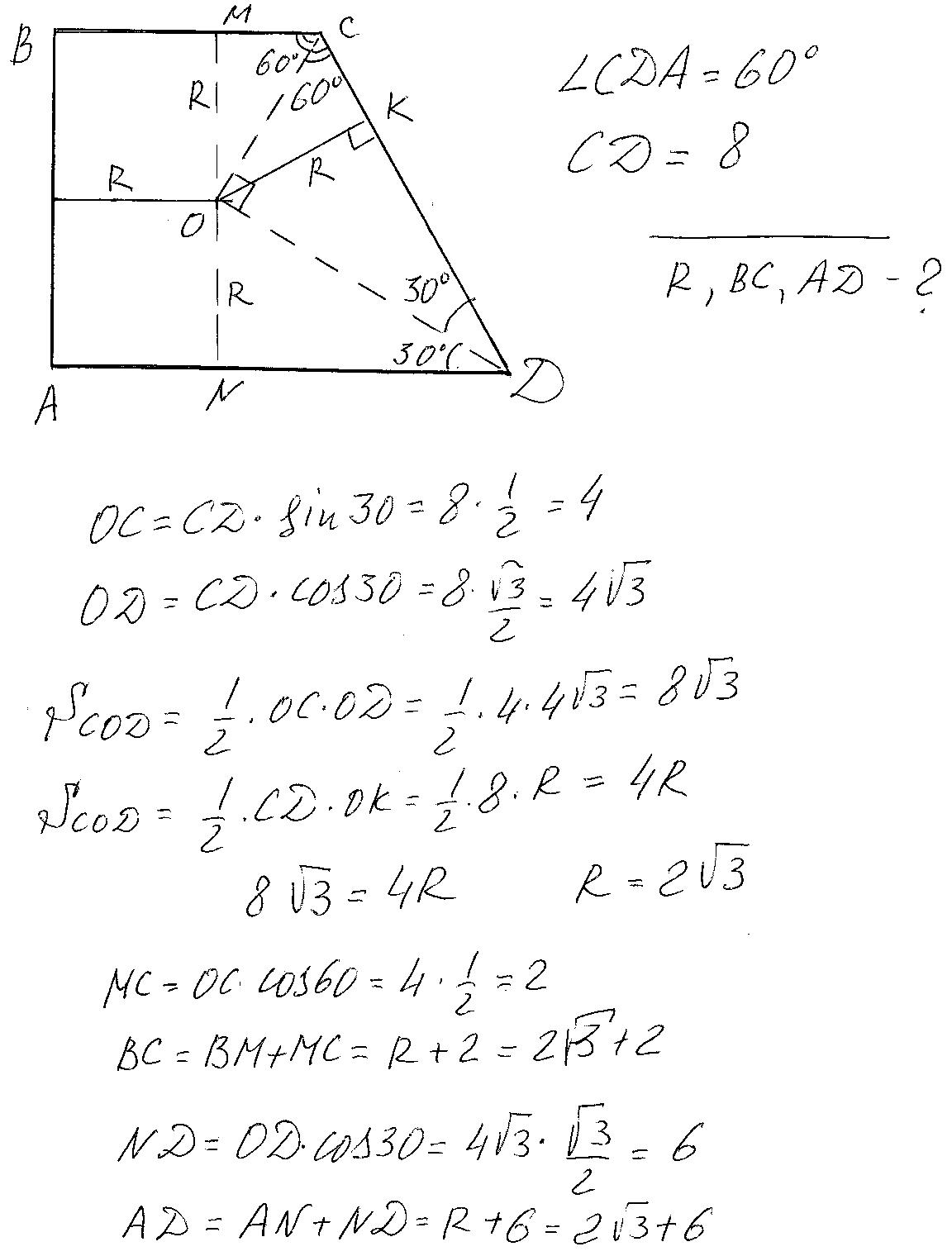
В прямоугольной трапеции один из углов 60 градусов, а большая боковая сторона 8 см. Найти основание трапеции и радиус вписанной в неё окружности.
Ответы
Ответ дал:
0
Из центра вписанной окружности О проведём радиусы ОМ, ОК, ОN(смотри рисунок). ОС и ОД -это гипотенузы прямоугольных треугольников и одновременно биссеуктрисы углов С и Д соответственно. Это вытекает из равенства треугольников ОМС и ОКС и ОNД и ОКД. Треугольник СОД всегда будет прямоугольным при любых значениях СД. Поскольку сумма углов трапеции прилежащих к одной стороне =180, а углы ОСД и ОДК вместе равны их полусумме, то есть=90, следовательно угол СОД=90. Дальше-просто тригонометрия.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад